在图形中行走

本节提供了斯坦利书中第一章的一些例子 [Stanley2013].

我们首先创建一个具有4个顶点的图：：

sage: G = Graph(4)
sage: G
Graph on 4 vertices

此图尚无边：：

sage: G.vertices(sort=True)
[0, 1, 2, 3]
sage: G.edges(sort=True)
[]

在我们可以添加边之前，我们需要告诉Sage，我们的图可以有循环和多条边。

sage: G.allow_loops(True)
sage: G.allow_multiple_edges(True)

现在，我们可以通过指定由边连接的顶点元组来添加边。如果有多条边，则需要添加具有重数的元组。：：

sage: G.add_edges([(0,0),(0,0),(0,1),(0,3),(1,3),(1,3)])

现在让我们看一下图表！：：

sage: G.plot()
Graphics object consisting of 11 graphics primitives

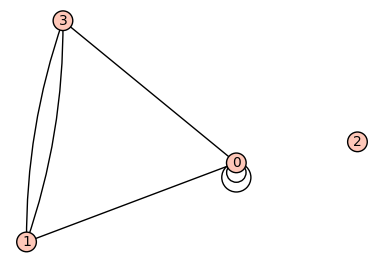
我们可以构造邻接矩阵：：

sage: A = G.adjacency_matrix()
sage: A
[2 1 0 1]
[1 0 0 2]
[0 0 0 0]
[1 2 0 0]

行中的条目 i 和列 j 的 ell -的次方 A 给出了长度的路径数 ell 从顶点 i 到顶点 j 。让我们验证一下：：

sage: A**2
[6 4 0 4]
[4 5 0 1]
[0 0 0 0]
[4 1 0 5]

从顶点开始有4条长度为2的路径 0 到顶点 1 ：在以下位置进行任一循环 0 然后是边缘 (0, 1) (两个选择)或占据优势 (0, 3) 然后两条边中的任何一条 (3, 1) (两种选择)：

sage: (A**2)[0,1]
4

为了计算闭合步行的数量，我们还可以查看 ell -阶本征值的幂。尽管本征值不是整数，但我们发现它们的平方和是一个整数：

sage: A.eigenvalues()
[0, -2, 0.5857864376269049?, 3.414213562373095?]
sage: sum(la**2 for la in A.eigenvalues())
16.00000000000000?

我们可以通过观察 ell -矩阵的次方：：

sage: (A**2).trace()
16