杨格和RSK算法¶
本节提供了一些有关Young格和RSK(Robinson-Schensted-Knuth)算法的例子,如Stanley的书的第8章所述 [Stanley2013].
杨氏点阵¶
我们从创建杨格的前几个能级开始 Y 。为此,我们需要定义偏序集的元素和顺序关系,它是分区的包容:
sage: level = 6
sage: elements = [b for n in range(level) for b in Partitions(n)]
sage: ord = lambda x,y: y.contains(x)
sage: Y = Poset((elements,ord), facade=True)
sage: H = Y.hasse_diagram()
当出现以下情况时,生成的图像效果最佳 dot2tex 已安装::
sage: view(H) # not tested
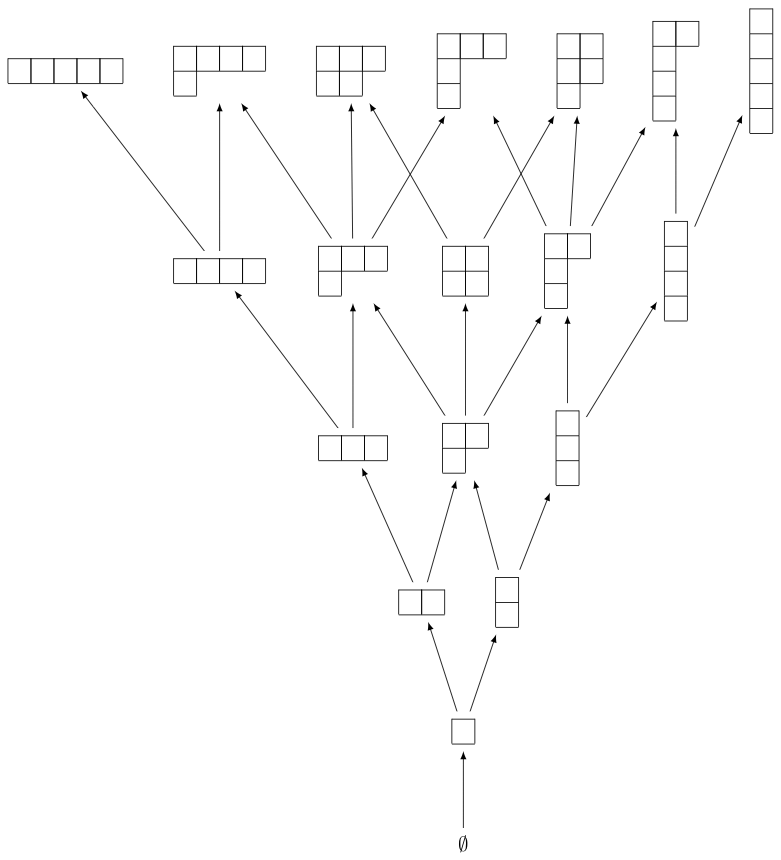
现在我们可以定义向上和向下运算符 U 和 D 在……上面 QQ Y 。首先,我们对分区执行此操作,这些分区构成了 QQ Y **
sage: QQY = CombinatorialFreeModule(QQ,elements)
sage: def U_on_basis(la):
....: covers = Y.upper_covers(la)
....: return QQY.sum_of_monomials(covers)
sage: def D_on_basis(la):
....: covers = Y.lower_covers(la)
....: return QQY.sum_of_monomials(covers)
作为一种速记,人们也可以将上述内容写成::
sage: U_on_basis = QQY.sum_of_monomials * Y.upper_covers
sage: D_on_basis = QQY.sum_of_monomials * Y.lower_covers
以下是将运算符应用于分区时的结果 (2,1) **
sage: la = Partition([2,1])
sage: U_on_basis(la)
B[[2, 1, 1]] + B[[2, 2]] + B[[3, 1]]
sage: D_on_basis(la)
B[[1, 1]] + B[[2]]
现在,我们在上定义向上和向下运算符 QQ Y **
sage: U = QQY.module_morphism(U_on_basis)
sage: D = QQY.module_morphism(D_on_basis)
我们可以查一下身份 D_{i+1} U_i - U_{i-1} D_i = I_i 在的所有分区上显式 i=3 **
sage: for p in Partitions(3):
....: b = QQY(p)
....: assert D(U(b)) - U(D(b)) == b
We can also check that the coefficient of lambda vdash n in U^n(emptyset) is equal to the number of standard Young tableaux of shape lambda:
sage: u = QQY(Partition([]))
sage: for i in range(4):
....: u = U(u)
sage: u
B[[1, 1, 1, 1]] + 3*B[[2, 1, 1]] + 2*B[[2, 2]] + 3*B[[3, 1]] + B[[4]]
例如,标准Young画面的形状数量 (2,1,1) 是 3 **
sage: StandardTableaux([2,1,1]).cardinality()
3
我们可以在一般情况下进行测试:
sage: for la in u.support():
....: assert u[la] == StandardTableaux(la).cardinality()
我们还可以对照钩长公式(定理8.1)进行检验:
sage: def hook_length_formula(p):
....: n = p.size()
....: return factorial(n) // prod(p.hook_length(*c) for c in p.cells())
sage: for la in u.support():
....: assert u[la] == hook_length_formula(la)
RSK算法¶
现在让我们转向RSK算法。我们可以按如下方式验证示例8.12:
sage: p = Permutation([4,2,7,3,6,1,5])
sage: RSK(p)
[[[1, 3, 5], [2, 6], [4, 7]], [[1, 3, 5], [2, 4], [6, 7]]]
Tableaux也可以显示为Tableaux::
sage: P,Q = RSK(p)
sage: P.pp()
1 3 5
2 6
4 7
sage: Q.pp()
1 3 5
2 4
6 7
反向RSK算法的实现如下:
sage: RSK_inverse(P,Q, output='permutation')
[4, 2, 7, 3, 6, 1, 5]
我们可以验证RSK算法是一个双射::
sage: def check_RSK(n):
....: for p in Permutations(n):
....: assert RSK_inverse(*RSK(p), output='permutation') == p
sage: for n in range(5):
....: check_RSK(n)