惠斯通电桥

惠斯通电桥是电子测量电路中应用的一种重要的组合电路。包括平衡的惠斯通电桥和非平衡的惠斯通电桥。本节将介绍惠斯通电桥的原理及应用。

一． 平衡的惠斯通电桥   

惠斯通电桥电路如图1所示。电路由4个电阻臂、1个直流电流源和1个检流计组成。（检流计类似于灵敏电流表，指针可以左右偏转，当指针指向中心位置时，表明通过检流计的电流为0）。

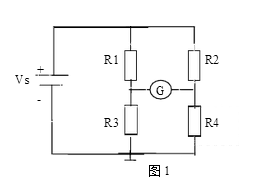
当检流计G不偏转时，这时流过检流表的电流为零。则电桥的电压比肯定相等：

根据欧姆定律可替代为：

因为检流表中电流为零，所以

得到

这里可以把惠斯通电桥平衡的关键总结为：      

惠斯通电桥平衡的条件是对角线电阻的乘积相等  

二．非平衡惠斯通电桥       下面介绍非平衡的惠斯通电桥，如图2所示。

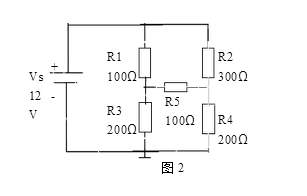
因为图2中电阻不满足上面（*）式的条件，所以图2所示的电路为非平衡电桥。下面用戴维南定理分析一下电路，求的通过R5的电流。

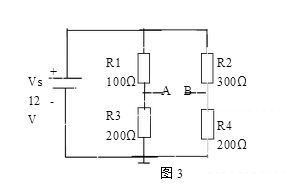
因为图2中电阻不满足上面（*）式的条件，所以图2所示的电路为非平衡电桥。下面用戴维南定理分析一下电路，求的通过R5的电流。    求得负载电流，必须用一个等效电路去代替电路的其他部分。所以将原电路分成两部分：A与地之间的戴维南等效电路，以及B与地之间的戴维南等效电路，然后再合并这两个戴维南电路。 

首先，先分析A点与地之间的戴维南等效电路。如图3所示，可知A点与地之间的电压Ua就是电阻R3上的电压。

=

再分析A点的等效电阻，把电压源短路，内阻为零，如图4所示，因为R2与R4短路，可 得A点的等效电阻 

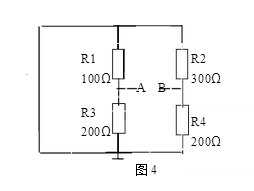
=100/200=66.7

按照相同的方法分析B点，得到B点的等效电压与等效电阻

= =4.8V

与 短路，因此， =300/200

最后把这两个戴维南等效电路代替原来的惠斯通电桥，并把负载 放在A与B之间。如图5示。 

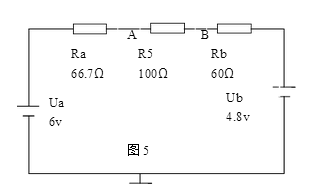
这时，可求得流过负载 的电流。因为 与 反向，因此净激励电压为 =1.2V

回路总电阻为R=

=

由欧姆定律可得：

=1.2/226.7(A)=5.29(mA)