摘要: 线性插值法 为了研究函数的变化规律,往往需要求出不在表上的函数值。因此,我们希望可以根据给定的函数表做一个既能反映函数f(x)的特性,又便于计算的简单函数P(x)。用P(x)近似f(X)。通常选一类简单的函数作为P(x),并使\(P(xi)=f(xi)\)对\...
线性插值法
为了研究函数的变化规律,往往需要求出不在表上的函数值。因此,我们希望可以根据给定的函数表做一个既能反映函数f(x)的特性,又便于计算的简单函数P(x)。用P(x)近似f(X)。通常选一类简单的函数作为P(x),并使\(P(xi)=f(xi)\)对\(i=1,2,……,n\)成立。这样确定下来的P(x)就是我们希望的插值函数,此即为插值法。
如何进行线性插值
假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的y值。
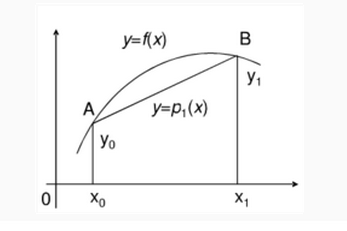
根据图中所示,我们得到\((y-y0)(x1-x0)=(y1-y0)(x-x0)\)
假设方程两边的值为α,那么这个值就是插值系数—从x0到x的距离与从x0到x1距离的比值。由于x值已知,所以可以从公式得到α的值
\(α=(x-x0)/(x1-x0)\)
同样,\(α=(y-y0)/(y1-y0)\)
这样,在代数上就可以表示成为:
\(y = (1- α)y0 + αy1\)
或者,
\(y = y0 + α(y1 - y0)\)
这样通过α就可以直接得到 y。实际上,即使x不在x0到x1之间并且α也不是介于0到1之间,这个公式也是成立的。在这种情况下,这种方法叫作线性外插—参见 外插值。
已知y求x的过程与以上过程相同,只是x与y要进行交换。
