合成孔径雷达处理¶
本节介绍如何使用与SAR处理相关的应用程序。
定标¶
SAR校准应用程序可以处理来自四个雷达传感器的数据校准:RadarSat2、Sentinel1、Cosmo-SkyMed和TerraSAR-X。
例如:
如果SARimg.tif是TerraSAR-X或Cosmo-SkyMed图像:
otbcli_SARCalibration -in SARimg.tif
-out SARimg-calibrated.tif
如果SARimg.tif是RadarSat2或Sentinel1图像,则可以指定查找表(在随此类图像提供的元数据中自动找到):
otbcli_SARCalibration -in SARimg.tif
-lut gamma
-out SARimg-calibrated.tif
对于TerraSAR-X(以及即将用于RadarSat2和Sentinel1),也可以使用噪声LUT来得出校准的噪声分布:
otbcli_SARCalibration -in SARimg.tif
-lut gamma -removenoise 1
-out SARimg-calibrated.tif
去斑点¶
合成孔径雷达图像通常会受到斑点噪声的干扰。为了抑制相干斑,改善雷达图像分析,人们提出了许多滤波技术。该模块实现了著名的去斑法:Frost、Lee、Gamma-MAP和Kuan。
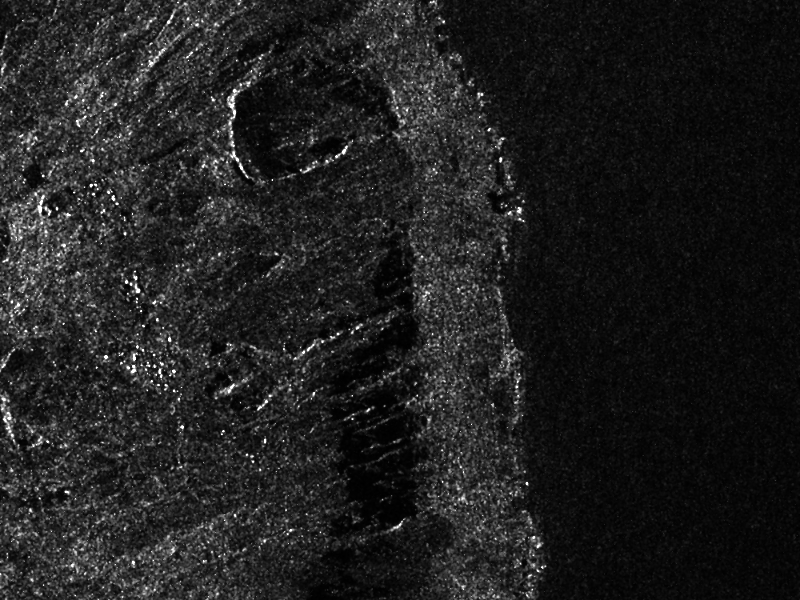
图( [ffig:S1VVdespeckledextract] 显示了在佛得角拍摄的SLC Sentinel1图像的摘录,波段VV和伽马滤镜的结果。以下命令用于生成去除斑点的摘录:
首先,将原始图像转换为强度1(实部对应于带1,虚部对应于带2):
otbcli_BandMath -il S1-VV-extract.tif
-exp im1b1^2+im1b2^2
-out S1-VV-extract-int.tif
然后使用Gamma-map过滤器去除强度图像的斑点:
otbcli_Despeckle -in S1-VV-extract-int.tif
-filter.gammamap.rad 5
-filter.gammamap.nblooks 1
-out S1-VV-despeckled-extract.tif
然后将产生的图像重新缩放到0到255的强度范围以进行显示。
旋光法¶
在传统的成像雷达中,测量是一个标量,它与在特定的线极化(HH、HV、VH或VV)组合下接收的反向散射功率成正比。旋光法是对这种测量的偏振进行测量和解释。它允许测量一种材料的各种光学性质。在旋光法中,基本的测量是 2x2 产生八维测量空间的复散射矩阵(辛克莱矩阵)。对于互惠目标,其中 HV=VH ,这个空间被压缩到五个维度:三个振幅 (|HH| , |HV| ,以及 |VV| );以及两相测量,(co-Poll:HH-VV和Cross-Poll:HH-HV)。(见 grss-ieee )。
矩阵转换¶
这种应用允许将经典极化矩阵相互转换。例如,可以从辛克莱矩阵得到相干矩阵,或者从相干矩阵得到米勒矩阵。下图( [fig:polconv] )显示了此应用程序中使用的工作流。
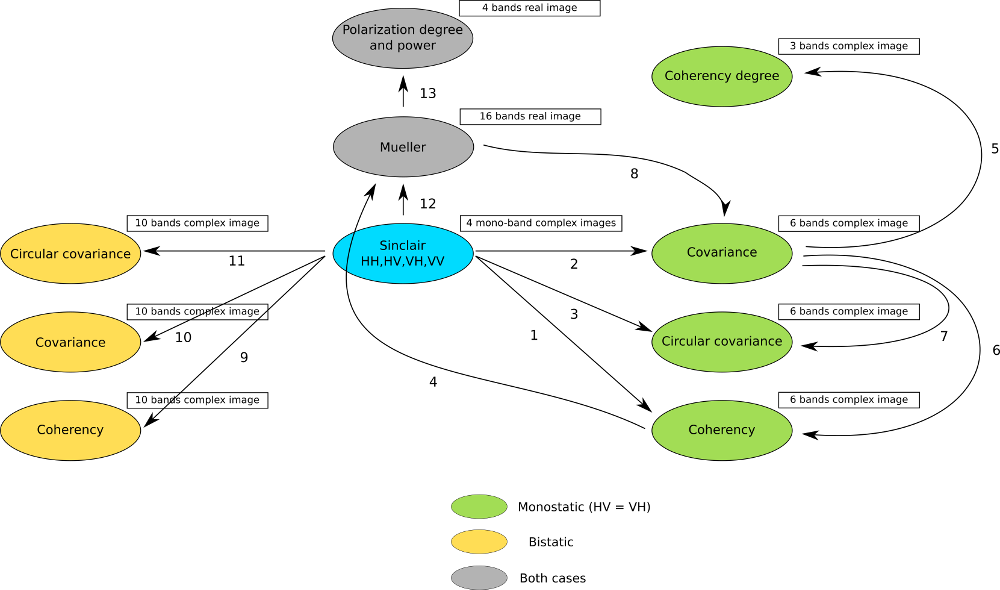
这个应用程序中使用的滤镜从不处理矩阵,而是处理每个波段与其元素相关的图像。由于在大多数情况下,SAR极化测量处理的是对称矩阵,因此只存储相关元素,因此代表它们的图像具有最小数量的波段。例如,相干矩阵的大小在单站情况下为3x3,在双站情况下为4x4:因此,它将被存储在6波段或10波段复数图像(矩阵的对角线和上部元素)中。
辛克莱矩阵是一个特例:它总是被表示为3或4个单波段复数图像(对于单基地或双基地情况)。
有13种可用转换,每一种都与以下参数相关:
- 最大限度地保持连贯
- 协方差最小
- 最小脉动与脉动方差
- 多相干性细胞监控器
- 协方差与连贯度
- 协方差与一致性
- 线性协方差对循环协方差
- 多层协方差
- 语音级到连贯性
- 正弦协方差
- 正弦环协方差
- 正弦推进器
- 马勒地形图功率
对于每个选项参数,下表给出了使用的公式。
-单声道情况-
MsinclairtocoherencyMatrixFunctor(SclairToReciproalCoherencyMatrixFunctor)
- 0.5 . (S_{hh}+S_{vv}).(S_{hh}+S_{vv})^{*}
- 0.5 . (S_{hh}+S_{vv}).(S_{hh}-S_{vv})^{*}
- 0.5 . (S_{hh}+S_{vv}).(2 S_{hv})^{*}
- 0.5 . (S_{hh}-S_{vv}).(S_{hh}-S_{vv})^{*}
- 0.5 . (S_{hh}-S_{vv}).(2 S_{hv})^{*}
- 0.5 . (2 S_{hv}).(2 S_{hv})^{*}
最小方差协方差(辛克莱到互惠协方差矩阵函数)
- S_{hh}.S_{hh}^{*}
- \sqrt{2}.S_{hh}.S_{hv}^{*}
- S_{hh}.S_{vv}^{*}
- 2.S_{hv}.S_{hv}^{*}
- \sqrt{2}.S_{hv}.S_{vv}^{*}
- S_{vv}.S_{vv}^{*}
最小径向协方差(SinclairToReciprocalCircularCovarianceMatrixFunctor)
- S_{ll}.S_{ll}^{*}
- S_{ll}.S_{lr}^{*}
- S_{ll}.S_{rr}^{*}
- S_{lr}.S_{lr}^{*}
- S_{lr}.S_{rr}^{*}
- S_{rr}.S_{rr}^{*}
有:
- S_{ll} = 0.5(S_{hh}+2j S_{hv}-S_{vv})
- S_{lr} = 0.5(j S_{hh}+j S_{vv})
- S_{rr} = 0.5(-S_{hh}+2j S_{hv}+S_{vv})
多相干性对(ReciprocalCoherencyToReciprocalMuellerFunctor)的影响
- 0.5*( C_{11}+C_{22}+C_{33} )
- Re(C_{12}) + Im(C_{22})
- Re(C_{13})
- Im(C_{23})
- Re(C_{12})
- 0.5*( C_{11}+C_{22}-C_{33} )
- Re(C_{23})
- Im(C_{13})
- -Re(C_{13})
- -Re(C_{23})
- 0.5.Re(VAL1)
- 0.5.Im(VAL0)
- Im(C_{23})
- Im(C_{13})
- 0.5.Im(VAL1^{*})
- 0.5.Re(VAL0)
有:
- VAL0 = C_{33}+C_{12}-C_{11}-(C_{12}-C_{22})^{*}
- VAL1 = -C_{33}+C_{12}-C_{11}-(C_{12}-C_{22})^{*}
哪里 C_{ij} 与互易相干矩阵的元素相关。
协方差与一致性程度(ReciprocalCovarianceToCoherencyDegreeFunctor)
- abs(S_{hh}.S_{vv}^{*}) / sqrt(S_{hh}.S_{hh}^{*}) / sqrt(S_{vv}.S_{vv}^{*})
- abs(S_{hv}.S_{vv}^{*}) / sqrt(S_{hv}.S_{hv}^{*}) / sqrt(S_{vv}.S_{vv}^{*})
- abs(S_{hh}.S_{hv}^{*}) / sqrt(S_{hh}.S_{hh}^{*}) / sqrt(S_{hv}.S_{hv}^{*})
协方差与一致性(ReciprocalCovarianceToReciprocalCoherencyFunctor)
- 0.5 . ( C_{33} + C_{13} + C_{13}^{*} + C_{11} )
- 0.5 . ( -C_{33} - C_{13} + C_{13}^{*} + C_{11} )
- 0.5 . ( \sqrt{2}.C_{12} + \sqrt{2}.C_{23}^{*} )
- 0.5 . ( C_{33} - C_{13} - C_{13}^{*} + C_{11} )
- 0.5 . ( \sqrt{2}.C_{12} - \sqrt{2}.C_{23}^{*} )
- 0.5 . ( 2 . C_{22} )
哪里 C_{ij} 与倒数线性协方差矩阵的元素有关。
多线性协方差对循环协方差(ReciprocalLinearCovarianceToReciprocalCircularCovarianceFunctor)
- 0.25 . ( C_{33}-i.\sqrt{2}.C_{23}-C_{13}+i.\sqrt{2}.C_{23}^{*}-C_{13}^{*}+2.C_{22}-i.\sqrt{2}.C_{12}+i.\sqrt{2}.C_{12}^{*}+C_{11} )
- 0.25 . ( i.\sqrt{2}.C_{33}+2.C_{23}-i.\sqrt{2}.C_{13}+i.\sqrt{2}.C_{13}^{*}+2.C_{12}^{*}-i.\sqrt{2}.C_{11} )
- 0.25 . ( -C_{33}+i.\sqrt{2}.C_{23}+C_{13}+i.\sqrt{2}.C_{23}^{*}+C_{13}^{*}+2.C_{22}-i.\sqrt{2}.C_{12}-i.\sqrt{2}.C_{12}^{*}-C_{11} )
- 0.25 . ( 2.C_{33}+2.C_{13}+2.C_{13}^{*}+2.C_{11} )
- 0.25 . ( i.\sqrt{2}.C_{33}+i.\sqrt{2}.C_{13}+2.C_{23}^{*}-i.\sqrt{2}.C_{13}^{*}+2.C_{12}-i.\sqrt{2}.C_{11} )
- 0.25 . ( C_{33}+i.\sqrt{2}.C_{23}-C_{13}-i.\sqrt{2}.C_{23}^{*}-C_{13}^{*}+2.C_{22}+i.\sqrt{2}.C_{12}-i.\sqrt{2}.C_{12}^{*}+C_{11} )
哪里 C_{ij} 与倒数线性协方差矩阵的元素有关。
MUELLER协方差(MUELERTO ReciprocalCoVarianceFunctor)
- 0.5.(M_{11}+M_{22}+2.M_{12})
- 0.5.\sqrt{2}.[(M_{13}+M_{23}) + j.(M_{14}+M_{24})]
- -0.5.(M_{33}+M_{44}) - j.M_{34}
- M_{11}-M_{22}
- 0.5.\sqrt{2}.[(M_{13}-M_{23}) + j.(M_{14}-M_{24})]
- 0.5.(M_{11}+M_{22}-2.M_{12})
-双基地情况-
Bsinclairto coherency(SclairToCoherencyMatrixFunctor)
- (S_{hh}+S_{vv}).(S_{hh}+S_{vv})^{*}
- (S_{hh}+S_{vv}).(S_{hh}-S_{vv})^{*}
- (S_{hh}+S_{vv}).(S_{hv}+S_{vh})^{*}
- (S_{hh}+S_{vv}).( j (S_{hv}-S_{vh}))^{*}
- (S_{hh}-S_{vv}).(S_{hh}-S_{vv})^{*}
- (S_{hh}-S_{vv}).(S_{hv}+S_{vh})^{*}
- (S_{hh}-S_{vv}).( j (S_{hv}-S_{vh}))^{*}
- (S_{hv}+S_{vh}).(S_{hv}+S_{vh})^{*}
- (S_{hv}+S_{vh}).( j (S_{hv}-S_{vh}))^{*}
- j (S_{hv}-S_{vh}).( j (S_{hv}-S_{vh}))^{*}
Bsinclairtocovarance(辛克莱到协方差MatrixFunctor)
- S_{hh}.S_{hh}^{*}
- S_{hh}.S_{hv}^{*}
- S_{hh}.S_{vh}^{*}
- S_{hh}.S_{vv}^{*}
- S_{hv}.S_{hv}^{*}
- S_{hv}.S_{vh}^{*}
- S_{hv}.S_{vv}^{*}
- S_{vh}.S_{vh}^{*}
- S_{vh}.S_{vv}^{*}
- S_{vv}.S_{vv}^{*}
BsinclairtoCircularCovarance(SclairToCircularCovaranceMatrixFunctor)
- S_{ll}.S_{ll}^{*}
- S_{ll}.S_{lr}^{*}
- S_{ll}.S_{rl}^{*}
- S_{ll}.S_{rr}^{*}
- S_{lr}.S_{lr}^{*}
- S_{lr}.S_{rl}^{*}
- S_{lr}.S_{rr}^{*}
- S_{rl}.S_{rl}^{*}
- S_{rl}.S_{rr}^{*}
- S_{rr}.S_{rr}^{*}
有:
- S_{ll} = 0.5(S_{hh}+j S_{hv}+j S_{vh}-S_{vv})
- S_{lr} = 0.5(j S_{hh}+S_{hv}-S_{vh}+j S_{vv})
- S_{rl} = 0.5(j S_{hh}-S_{hv}+ S_{vh}+j S_{vv})
- S_{rr} = 0.5(-S_{hh}+j S_{hv}+j S_{vh}+S_{vv})
-这两起案件-
辛克莱尔托穆勒(辛克莱·托穆勒)
- 0.5 Re( T_{xx}.T_{xx}^{*} + T_{xy}.T_{xy}^{*} + T_{yx}.T_{yx}^{*} + T_{yy}.T_{yy}^{*} )
- 0.5 Re( T_{xx}.T_{xx}^{*} - T_{xy}.T_{xy}^{*} + T_{yx}.T_{yx}^{*} - T_{yy}.T_{yy}^{*} )
- Re( T_{xx}.T_{xy}^{*} + T_{yx}.T_{yy}^{*} )
- Im( T_{xx}.T_{xy}^{*} + T_{yx}.T_{yy}^{*} )
- 0.5 Re( T_{xx}.T_{xx}^{*} + T_{xy}.T_{xy}^{*} - T_{yx}.T_{yx}^{*} - T_{yy}.T_{yy}^{*} )
- 0.5 Re( T_{xx}.T_{xx}^{*} - T_{xy}.T_{xy}^{*} - T_{yx}.T_{yx}^{*} + T_{yy}.T_{yy}^{*} )
- Re( T_{xx}.T_{xy}^{*} - T_{yx}.T_{yy}^{*} )
- Im( T_{xx}.T_{xy}^{*} - T_{yx}.T_{yy}^{*} )
- Re( T_{xx}.T_{yx}^{*} + T_{xy}.T_{yy}^{*} )
- Im( T_{xx}.T_{yx}^{*} - T_{xy}.T_{yy}^{*} )
- Re( T_{xx}.T_{yy}^{*} + T_{xy}.T_{yx}^{*} )
- Im( T_{xx}.T_{yy}^{*} - T_{xy}.T_{yx}^{*} )
- Re( T_{xx}.T_{yx}^{*} + T_{xy}.T_{yy}^{*} )
- Im( T_{xx}.T_{yx}^{*} - T_{xy}.T_{yy}^{*} )
- Re( T_{xx}.T_{yy}^{*} + T_{xy}.T_{yx}^{*} )
- Im( T_{xx}.T_{yy}^{*} - T_{xy}.T_{yx}^{*} )
有:
- T_{xx} = -S_{hh}
- T_{xy} = -S_{hv}
- T_{yx} = S_{vh}
- T_{yy} = S_{vv}
MuellerTopolandPower(MuellerToPolarisationDegreeAndPowerFunctor)
- P_{min}
- P_{max}
- DegP_{min}
- DegP_{max}
例如:
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invv imageryC_VV.tif -conv msinclairtocoherency -outc coherency.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invv imageryC_VV.tif -conv msinclairtocovariance -outc covariance.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invv imageryC_VV.tif -conv msinclairtocircovariance -outc circ_covariance.tif
otbcli_SARPolarMatrixConvert -inc coherency.tif -conv mcoherencytomueller -outf mueller.tif
otbcli_SARPolarMatrixConvert -inc covariance.tif -conv mcovariancetocoherencydegree -outc coherency_degree.tif
otbcli_SARPolarMatrixConvert -inc covariance.tif -conv mcovariancetocoherency -outc coherency.tif
otbcli_SARPolarMatrixConvert -inc covariance.tif -conv mlinearcovariancetocircularcovariance -outc circ_covariance.tif
otbcli_SARPolarMatrixConvert -inf mueller.tif -conv muellertomcovariance -outc covariance.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invh imageryC_VH.tif -invv imageryC_VV.tif -conv bsinclairtocoherency -outc bcoherency.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invh imageryC_VH.tif -invv imageryC_VV.tif -conv bsinclairtocovariance -outc bcovariance.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invh imageryC_VH.tif -invv imageryC_VV.tif -conv bsinclairtocircovariance -outc circ_bcovariance.tif
otbcli_SARPolarMatrixConvert -inhh imageryC_HH.tif -inhv imageryC_HV.tif -invh imageryC_VH.tif -invv imageryC_VV.tif -conv sinclairtomueller -outf mueller.tif
otbcli_SARPolarMatrixConvert -inf mueller.tif -conv muellertopoldegandpower -outf degreepower.tif
旋光分解¶
从单波段复数图像(HH、HV、VH、VV)返回选定的分解。H-Alpha-A分解是目前唯一可用的分解;它是针对单站情况(发射机和接收机位于同一位置)实现的。用户必须提供三个单波段复数图像HH、HV或VH和VV(单站情况下HV=VH)。H-α-A分解包括平均3x3复相干矩阵(非相干分析):由于参数inco.kernelSize,用户必须提供平均窗口的大小。这些应用程序返回一个浮点向量图像,由三个通道组成:H(熵)、Alpha、A(各向异性)。
以下是使用的公式(请参考上一节关于如何从辛克莱获得相干矩阵的内容):
- entropy = -\sum_{i=0}^{2} \frac{p[i].\log{p[i]}}{\log{3}}
- \alpha = \sum_{i=0}^{2} p[i].\alpha_{i}
- anisotropy = \frac {SortedEigenValues[1] - SortedEigenValues[2]}{SortedEigenValues[1] + SortedEigenValues[2]}
在哪里:
- p[i] = max(SortedEigenValues[i], 0) / \sum_{i=0}^{2, SortedEigenValues[i]>0} SortedEigenValues[i]
- \alpha_{i} = \left| SortedEigenVector[i] \right|* \frac{180}{\pi}
示例:
我们首先从原始图像中提取ROI(不是必需的)。这里,Imagery_HH.tif表示辛克莱矩阵的元素HH(依此类推)。
otbcli_ExtractROI -in imagery_HH.tif -out imagery_HH_extract.tif -startx 0 -starty 0 -sizex 1000 -sizey 1000
otbcli_ExtractROI -in imagery_HV.tif -out imagery_HV_extract.tif -startx 0 -starty 0 -sizex 1000 -sizey 1000
otbcli_ExtractROI -in imagery_VV.tif -out imagery_VV_extract.tif -startx 0 -starty 0 -sizex 1000 -sizey 1000
接下来,我们应用H-Alpha-A分解:
otbcli_SARDecompositions -inhh imagery_HH_extract.tif
-inhv imagery_HV_extract.tif
-invv imagery_VV_extract.tif
-decomp haa -inco.kernelsize 5
-out haa_extract.tif
结果有三个带:熵(0..1)-α(0..90)-各向异性(0..1)。它被分成3个单波段图像,这要归功于以下命令:
otbcli_SplitImage -in haa_extract.tif -out haa_extract_splitted.tif
多亏了一个颜色查询表,每一张图像都被涂上了颜色。请注意如何为每个偏振变量提供最小值和最大值。
otbcli_ColorMapping -in haa_extract_splitted_0.tif -method continuous -method.continuous.lut hot -method.continuous.min 0 -method.continuous.max 1 -out entropy_hot.tif uint8
otbcli_ColorMapping -in haa_extract_splitted_1.tif -method continuous -method.continuous.lut hot -method.continuous.min 0 -method.continuous.max 90 -out alpha_hot.tif uint8
otbcli_ColorMapping -in haa_extract_splitted_2.tif -method continuous -method.continuous.lut hot -method.continuous.min 0 -method.continuous.max 1 -out anisotropy_hot.tif uint8
结果如下图所示( [fig:entropyimage] , [fig:alphaimage] 和 [fig:anisotropyimage] )。



旋光合成器¶
这个应用程序为每个像素提供了SAR系统接收的功率,其基数不同于经典的(H,V)基数(极化合成)。由于取向(Psi)和椭圆度(Khi)参数,新的基由用户定义的两个琼斯向量来表示。这些参数是PSII、KHII、PSIR和KHIR。后缀(I)和(R)分别指发射天线和接收天线。方向和椭圆度以度为单位,分别在-90/90度和-45/45度之间。
可以处理四种偏振架构:
- HH_HV_VH_VV:全极化,一般双基地情况。
- HH_HV_VV or HH_VH_VV: full polarization, monostatic case (transmitter and receiver are co-located).
- HHHV:双极化。
- VH_VV:双极化。
该应用程序将复杂的矢量图像作为输入,其中每个频段对应于特定的发射/接收极化方案。用户必须遵守上面给出的波段顺序,因为波段是用来构建辛克莱矩阵的。
为了确定架构,应用程序首先依赖于输入图像的波段数。
- 架构HH_HV_VH_VV是唯一一个有四个波段的,不存在可能的混淆。
- Concerning HH_HV_VV and HH_VH_VV architectures, both correspond to a three channels image. But they are processed in the same way, as the Sinclair matrix is symmetric in the monostatic case.
- 最后,最后两种架构(双极化)不能仅通过输入图像的波段数来区分。然后,用户必须使用参数EMISTH和EMISTV来指示系统的体系结构:对于HH_HV,EMISTH=1和EMISTV=0;对于VH_VV,EMISTH=0和EMISTV=1。
注:如果架构为HH_HV,则KHII和PSII自动设置为0/0度;如果架构为VH_VV,则KHII和PSII自动设置为0/90度。
也可以强制计算为共极或交叉极模式。在共极情况下,psir和khir的值将被忽略并强制为psii和khii;与交叉极模式相同,其中khir和psir将被强制为psii+90度和-khii。
最后,极化合成的结果通过一幅单波段标量图像在功率域中表示。
最终的公式如下: P=\mid B^T.[S].A\mid^2 ,其中A和B是两个琼斯向量,S是辛克莱矩阵。
The two figures below ([fig:polsynthll] and [fig:polsynthlr]) show the two images obtained with the basis LL and LR (L for left circular polarization and R for right polarization), from a Radarsat-2 image taken over Vancouver, Canada. Once the four two-band images imagery_HH imagery_HV imagery_VH imagery_VV were merged into a single four complex band image imageryC_HH_HV_VH_VV.tif, the following commands were used to produce the LL and LR images:
otbcli_SARPolarSynth -in imageryC_HH_HV_VH_VV.tif
-psii 0 -khii 45 -mode co
-out test-LL.tif
otbcli_SARPolarSynth -in imageryC_HH_HV_VH_VV.tif
-psii 0 -khii 45 -mode cross
-out test-LR.tif
然后将产生的图像重新缩放到0到255的强度范围以进行显示。


极化数据可视化¶
最后,让我们来谈谈极化数据可视化。极化数据可视化与将其分解为重要物理过程的方式之间有很强的联系。事实上,通过将这种分解的结果(或组合)设置为有助于解释SAR极化图像的RGB通道。
目前还没有特定的专用应用程序,但可以使用不同应用程序的组合作为替代。让我们在加利福尼亚州旧金山著名的金门大桥上空进行RADARSAT-2采购。
我们首先从原始图像中提取(非强制)。
otbcli_ExtractROI -in imagery_HH.tif -out imagery_HH_extract.tif -startx 0 -starty 6300 -sizex 2790 -sizey 2400
otbcli_ExtractROI -in imagery_HV.tif -out imagery_HV_extract.tif -startx 0 -starty 6300 -sizex 2790 -sizey 2400
otbcli_ExtractROI -in imagery_VV.tif -out imagery_VV_extract.tif -startx 0 -starty 6300 -sizex 2790 -sizey 2400
然后,我们使用 BandMath 应用程序:
otbcli_BandMath -il imagery_HH_extract.tif -out HH.tif -exp "sqrt(im1b1^2+im1b2^2)"
otbcli_BandMath -il imagery_HV_extract.tif -out HV.tif -exp "sqrt(im1b1^2+im1b2^2)"
otbcli_BandMath -il imagery_VV_extract.tif -out VV.tif -exp "sqrt(im1b1^2+im1b2^2)"
请注意,BandMath应用程序将图像‘Imagery_XX_Extt.tif’解释为由两个波段组成的图像,其中第一个波段与信号的实部相关,第二个波段与虚部相关(这就是通过以下表达式获得模数的原因 im1b1^2+im1b2^2 )。
然后,我们将生成的图像重新调整为0到255之间的亮度:
otbcli_Rescale -in HH.tif -out HH_res.png uint8
otbcli_Rescale -in HV.tif -out HV_res.png uint8
otbcli_Rescale -in VV.tif -out VV_res.png uint8
下图( [fig:hhfrisco] , [fig:hvfrisco] 和 [fig:vvfrisco] )显示获取的图像:



现在最有趣的一步是。为了对这些数据进行友好的着色,我们将使用Pauli分解,定义如下:
- a=\frac{|S_{HH}-S_{VV}|}{\sqrt{2}}
- b=\sqrt{2}.|S_{HV}|
- c=\frac{|S_{HH}+S_{VV}|}{\sqrt{2}}
我们再次使用BandMath应用程序:
otbcli_BandMath -il imagery_HH_extract.tif imagery_HV_extract.tif imagery_VV_extract.tif -out Channel1.tif -exp "sqrt(((im1b1-im3b1)^2+(im1b2-im3b2)^2))"
otbcli_BandMath -il imagery_HH_extract.tif imagery_HV_extract.tif imagery_VV_extract.tif -out Channel2.tif -exp "sqrt(im2b1^2+im2b2^2)"
otbcli_BandMath -il imagery_HH_extract.tif imagery_HV_extract.tif imagery_VV_extract.tif -out Channel3.tif -exp "sqrt(((im1b1+im3b1)^2+(im1b2+im3b2)^2))"
请注意,我们故意省略了SQRT(2)因子,因为它们的影响将被重新调整步骤抵消。然后,我们将生成的图像重新调整为0到255之间的亮度:
otbcli_Rescale -in Channel1.tif -out Channel1_res.tif uint8
otbcli_Rescale -in Channel2.tif -out Channel2_res.tif uint8
otbcli_Rescale -in Channel3.tif -out Channel3_res.tif uint8
最后,我们将这三个波段合并成一幅RGB图像。
otbcli_ConcatenateImages -il Channel1_res.tif Channel2_res.tif Channel3_res.tif
-out visuPauli.png
结果如下图所示( [fig:colorfrisco] )。
