小波变换

在 0.9.1 版本加入: 仅在0.9.1版中添加了小波函数

我们将使用小波对图像进行变换，以使其大部分值为0(或更小)，但大部分信号保持不变。

本教程的代码可从源代码发行版获得，其格式为 mahotas/demos/wavelet_compression.py 。

我们从导入和加载输入图像开始

import numpy as np
import mahotas
import mahotas.demos

from mahotas.thresholding import soft_threshold
from matplotlib import pyplot as plt
from os import path
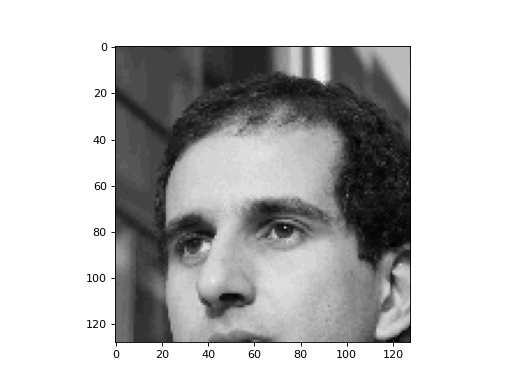
f = mahotas.demos.load('luispedro', as_grey=True)
f = f[:256,:256]
plt.gray()
# Show the data:
print("Fraction of zeros in original image: {0}".format(np.mean(f==0)))
plt.imshow(f)
plt.show()

(Source code, png, hires.png, pdf)

_images/wavelets-1.png

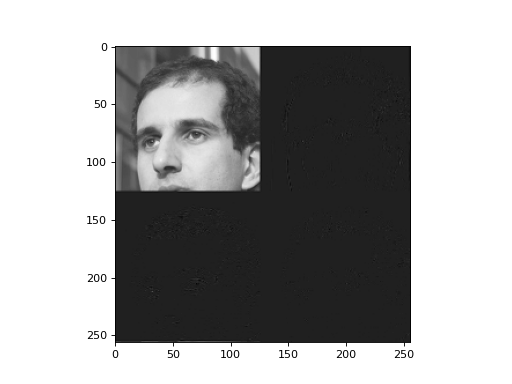
原始图像中没有零。我们现在尝试一种基线压缩方法：每隔一个像素保存一次，只保存高阶位。

direct = f[::2,::2].copy()
direct /= 8
direct = direct.astype(np.uint8)
print("Fraction of zeros in original image (after division by 8): {0}".format(np.mean(direct==0)))
plt.imshow(direct)
plt.show()

(Source code, png, hires.png, pdf)

_images/wavelets-2.png

不过，只有几个零。然而，我们已经扔掉了75%的价值。然而，使用相同数量的值，我们能得到更好的图像吗？

我们将使用Daubechies小波(D8)对图像进行变换，然后丢弃高位。

# Transform using D8 Wavelet to obtain transformed image t:
t = mahotas.daubechies(f,'D8')

# Discard low-order bits:
t /= 8
t = t.astype(np.int8)
print("Fraction of zeros in transform (after division by 8): {0}".format(np.mean(t==0)))
plt.imshow(t)
plt.show()

(Source code, png, hires.png, pdf)

_images/wavelets-3.png

这个有60%是零！重建的图像是什么样子的？

# Let us look at what this looks like
r = mahotas.idaubechies(t, 'D8')
plt.imshow(r)
plt.show()

(Source code, png, hires.png, pdf)

_images/wavelets-4.png

这是一个相当好的降低，没有太多的质量损失。我们可以走得更远，在转换后的空间中丢弃小的值。另外，让我们使剩余的值在大小上更小。

现在，这将是77%的零，其余的是小值。这幅图像将作为一幅无损图像压缩得很好，我们可以在传输后重建出完整的图像。质量当然比仅仅保留每四个像素和低阶位要高。

tt = soft_threshold(t, 12)
print("Fraction of zeros in transform (after division by 8 & soft thresholding): {0}".format(np.mean(tt==0)))
# Let us look again at what we have:
rt = mahotas.idaubechies(tt, 'D8')
plt.imshow(rt)

(Source code, png, hires.png, pdf)

_images/wavelets-5.png

那“边界”呢？

在本例中，我们可以看到边界上的一些人工制品。我们可以利用 wavelet_center 和 wavelet_decenter 要正确处理边框：

fc = mahotas.wavelet_center(f)
t = mahotas.daubechies(fc, 'D8')
r = mahotas.idaubechies(fc, 'D8')
rd = mahotas.wavelet_decenter(r, fc.shape)

Now, rd is equal (except for rounding) to fc without any border effects.

API文档

这是一个用Python语言编写的计算机视觉包。

主要特征

特征

计算全局和局部特征(几个子模块，包括SURF和Haralick特征)

卷积

卷积与小波

变形

形态特征。大多数是在mahotas级别提供的，包括腐蚀()、扩张()...

分水岭

种子分水岭实施

不读取/不保存

读/写图像

文档：https://mahotas.readthedocs.io/

引文：

科埃略，路易斯·佩德罗，2013年。Mahotas：用于可编写脚本的计算机视觉的开源软件。开放研究软件杂志，1：E3，DOI：https://dx.doi.org/10.5334/jors.ac

mahotas.daubechies(f, code, inline=False)

Daubechies小波变换

如果图像大小是2的幂，则此函数效果最好！

参数:
fNdarray

2-D图像

code应力

‘D2’，‘D4’，...《D20》

inline布尔值，可选

是否将结果写入输入图像。默认情况下，将返回新图像。整数图像始终转换为浮点数并进行复制。

参见

haar

函数Haar变换(等价于D2)

mahotas.haar(f, preserve_energy=True, inline=False)

哈尔变换

参数:
f二维ndarray

输入图像

preserve_energy布尔值，可选

是否将结果正常化以保存能量(默认设置)。

inline布尔值，可选

是否将结果写入输入图像。默认情况下，将返回新图像。整数图像始终转换为浮点数并进行复制。

参见

ihaar

函数逆Haar变换

mahotas.idaubechies(f, code, inline=False)

Daubechies小波逆变换

参数:
fNdarray

2-D图像

code应力

‘D2’，‘D4’，...《D20》

inline布尔值，可选

是否将结果写入输入图像。默认情况下，将返回新图像。整数图像始终转换为浮点数并进行复制。

参见

haar

函数Haar变换(等价于D2)

mahotas.ihaar(f, preserve_energy=True, inline=False)

逆Haar变换

ihaar(haar(f)) 大致等于 f (相同，除非可能存在舍入问题)。

参数:
f二维ndarray

输入图像。如果是整数图像，则转换为浮点(双精度)。

preserve_energy布尔值，可选

是否将结果正常化以保存能量(默认设置)。

inline布尔值，可选

是否将结果写入输入图像。默认情况下，将返回新图像。整数图像始终转换为浮点数并进行复制。

退货:
fNdarray

参见

haar

函数正向Haar变换