向量重建

例如，可以使用矢量重建算法来重建磁性样品内的磁化矢量场。

以下是有关如何使用矢量重建算法的示例 [B6] [A3] 使用 TomoPy ：引用：Gursoy：14a。

From a reconstructed 3D object to its projections and back

为了测试该算法，可以计算重建对象的投影，并从这些投影返回到重建的模型对象。最后，将矢量场重建的结果与初始目标进行比较。

本教程中使用的所有数据集均可在 tomoBank 。

首先，让我们进行必要的进口

import dxchange
import tomopy
import numpy as np
import matplotlib.pyplot as plt
import time

让我们加载对象：磁化矢量的三个分量贯穿整个对象。该对象将被填充，以便具有立方体对象。之后，将对其进行下采样以进行更快的计算。

obx = dxchange.read_tiff('M4R1_mx.tif').astype('float32')
oby = dxchange.read_tiff('M4R1_my.tif').astype('float32')
obz = dxchange.read_tiff('M4R1_mz.tif').astype('float32')


npad = ((182, 182), (64, 64), (0, 0))
obx = np.pad(obx, npad, mode='constant', constant_values=0)
oby = np.pad(oby, npad, mode='constant', constant_values=0)
obz = np.pad(obz, npad, mode='constant', constant_values=0)

obx = tomopy.downsample(obx, level=2, axis=0)
obx = tomopy.downsample(obx, level=2, axis=1)
obx = tomopy.downsample(obx, level=2, axis=2)

oby = tomopy.downsample(oby, level=2, axis=0)
oby = tomopy.downsample(oby, level=2, axis=1)
oby = tomopy.downsample(oby, level=2, axis=2)

obz = tomopy.downsample(obz, level=2, axis=0)
obz = tomopy.downsample(obz, level=2, axis=1)
obz = tomopy.downsample(obz, level=2, axis=2)

定义投影角度：从90度到270度的31个角度：

ang = tomopy.angles(31, 90, 270)

并计算绕三个垂直笛卡尔轴旋转的对象的投影：

prj1 = tomopy.project3(obx, oby, obz, ang, axis=0, pad=False)
prj2 = tomopy.project3(obx, oby, obz, ang, axis=1, pad=False)
prj3 = tomopy.project3(obx, oby, obz, ang, axis=2, pad=False)

给定投影的三个坐标可以可视化如下：

fig = plt.figure(figsize=(15, 8))
ax1 = fig.add_subplot(1, 3, 1)
ax1.imshow(obx[52,:,:])
ax2 = fig.add_subplot(1, 3, 2)
ax2.imshow(oby[52,:,:])
ax3 = fig.add_subplot(1, 3, 3)
ax3.imshow(obz[52,:,:])
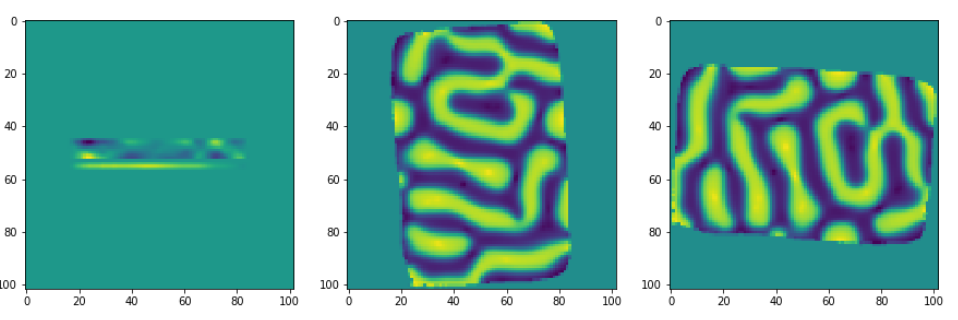
../_images/projections.png

最后，我们将重建矢量场分量，将我们根据第一个3D初始对象计算的投影作为输入。可以调整迭代次数以具有更快但更不精确的重建，或者具有更精确的重建。

rec1, rec2, rec3 = tomopy.vector3(prj1, prj2, prj3, ang, ang, ang, axis1=0, axis2=1, axis3=2, num_iter=100)
dxchange.write_tiff(rec1)
dxchange.write_tiff(rec2)
dxchange.write_tiff(rec3)

Comparison of results against input object

在本节中，我们将通过断层重建获得的矢量场分量的结果与作为输入的对象的矢量场分量进行比较：

第一磁化向量分量与输入数据对象的比较(对于给定片)。

fig = plt.figure(figsize=(9, 7))
ax1 = fig.add_subplot(1, 2, 1)
ax1.imshow(obx[52,:,:])
ax2 = fig.add_subplot(1, 2, 2)
ax2.imshow(rec1[52,:,:])
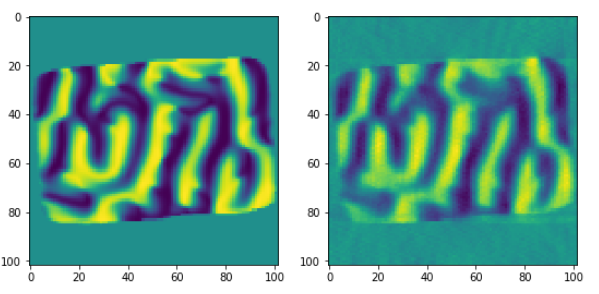
../_images/vector_compare_x.png

第二磁化矢量分量与输入数据对象的比较(对于给定片)：

fig = plt.figure(figsize=(9, 7))
ax1 = fig.add_subplot(1, 2, 1)
ax1.imshow(oby[52,:,:])
ax2 = fig.add_subplot(1, 2, 2)
ax2.imshow(rec2[52,:,:])
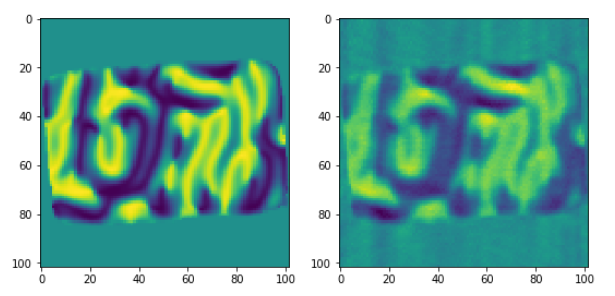
../_images/vector_compare_y.png

第三磁化向量分量与输入数据对象的比较(对于给定片)：

fig = plt.figure(figsize=(9, 7))
ax1 = fig.add_subplot(1, 2, 1)
ax1.imshow(obz[52,:,:])
ax2 = fig.add_subplot(1, 2, 2)
ax2.imshow(rec3[52,:,:])
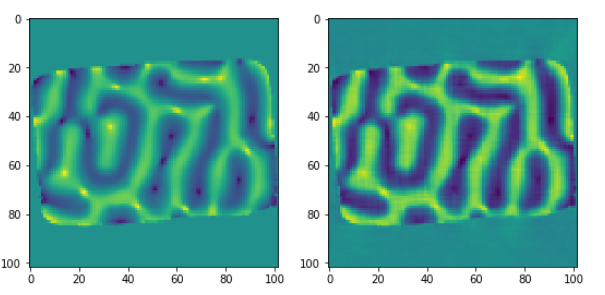
../_images/vector_compare_z.png

Other examples

在tomopy/doc/demo文件夹中可以找到三个jupyter笔记本，其中包含示例以及与矢量重建相关的一些数学概念：

使用向量3的示例：从3个垂直倾斜角度输入数据投影：

  • vectorrec_1.ipynb

  • vectorrec_disk.ipynb

使用向量2的示例：从两个垂直倾斜角度输入数据投影：

  • vector_heterostructure.ipynb

可以通过(从doc/demo文件夹)应用以下命令来构建矢量重建示例html幻灯片：

jupyter-nbconvert --to slides --post serve vectorrec_1.ipynb

jupyter-nbconvert --to slides --post serve vectorrec_disk.ipynb

jupyter-nbconvert --to slides --post serve vector_heterostructure.ipynb