线性规划(混合整数)

本文档通过举例说明Sage可以解决的几个问题，说明了线性规划(LP)和混合整数线性规划(MILP)在SAGE中的使用。给出的大多数例子都是出于图论的考虑，在没有这个领域的任何具体知识的情况下应该是可以理解的。作为组合学中的一个工具，使用线性规划相当于理解如何通过线性约束重新表述优化(或存在)问题。

这是这本书中一章的译文 Calcul mathematique avec Sage 。这本书现在存在于 English, too 。

定义

Here we present the usual definition of what a linear program is: it is defined by a matrix A: mathbb{R}^m mapsto mathbb{R}^n, along with two vectors b,c in mathbb{R}^n. Solving a linear program is searching for a vector x maximizing an objective function and satisfying a set of constraints, i.e.

\[C^t x=\max_{x‘\Text{so}Ax’\leq b}c^t x‘\]

在哪里订购 u leq u' 两个向量之间的关系意味着 u' 的条目数成对大于 u 。我们还写道：

\[\begin{split}\text{Max: } & c^t x\\ \text{Such that: } & Ax \leq b\end{split}\]

同样地，我们也可以说，求解一个线性规划相当于最大化一个定义在多面体上的线性函数(原图或 A^{-1} (leq b) )。然而，这些定义并没有告诉我们如何在组合学中使用线性规划。在接下来的内容中，我们将展示如何解决背包问题、最大匹配问题和流问题等优化问题。

混合整数线性规划

伴随着线性规划的定义而来的是坏消息：线性规划可以在多项式时间内求解。这确实是个坏消息，因为这将意味着，除非我们定义指数规模的LP，否则我们不能指望LP解决NP完全问题，这将是令人失望的。从好的方面来看，如果我们被允许指定不同类型的约束：要求某些变量是整数而不是实值，那么解线性规划就成了NP-完全的。这样的线性规划实际上被称为“混合整数线性规划”(有些变量可以是整数，有些是实数)。因此，我们可以预期在MILP框架中发现 wide 表现力的范围。

实用

这个 MILP 班级

这个 MILP Sage中的类代表一个MILP！它也可用于求解正则线性规划问题。它具有非常少的方法，用于定义我们的约束和变量集，然后在计算后读取求解器找到的解。还可以将使用Sage定义的MILP导出到 .lp 或 .mps 文件，大多数求解器都能理解。

让我们请Sage来解决以下LP：

\[\begin{split}\text{Max: } & x + y + 3z\\ \text{Such that: } & x + 2y \leq 4\\ \text{} & 5z - y \leq 8\\ \text{} & x,y,z \geq 0\\\end{split}\]

要实现这一点，我们需要定义一个对应的 MILP 对象，以及3个变量 x ， y 和 z **

sage: p = MixedIntegerLinearProgram()
sage: v = p.new_variable(real=True, nonnegative=True)
sage: x, y, z = v['x'], v['y'], v['z']

接下来，我们设置目标函数

sage: p.set_objective(x + y + 3*z)

最后，我们设置了约束

sage: p.add_constraint(x + 2*y <= 4)
sage: p.add_constraint(5*z - y <= 8)

这个 solve 方法默认情况下返回目标函数达到的最佳值

sage: round(p.solve(), 2)
8.8

我们可以读取求解器找到的最优分配 x ， y 和 z 通过 get_values 方法

sage: round(p.get_values(x), 2)
4.0
sage: round(p.get_values(y), 2)
0.0
sage: round(p.get_values(z), 2)
1.6

变数

在上例中，我们通过以下方式获取变量 v['x'] ， v['y'] 和 v['z'] 。也就是说，较大的LP/MILP将要求我们将一个LP变量与许多Sage对象相关联，这些对象可以是整数、字符串，甚至可以是图的顶点和边。例如：

sage: x = p.new_variable(real=True, nonnegative=True)

有了这个新对象 x 我们现在可以使用以下命令编写约束 x[1],...,x[15] 。

sage: p.add_constraint(x[1] + x[12] - x[14] >= 8)

请注意，我们不需要定义 x 。实际上， x 将接受任何不变的对象作为键，就像字典所做的那样。我们现在可以写下

sage: p.add_constraint(x["I am a valid key"] +
....:                  x[("a",pi)] <= 3)

因为任何不可变的对象都可以用作键，所以双重索引变量 x^{1,1}, ..., x^{1,15}, x^{2,1}, ..., x^{15,15} 可以由以下对象引用 x[1,1],...,x[1,15],x[2,1],...,x[15,15]

sage: p.add_constraint(x[3,2] + x[5] == 6)

类型化变量和界限

Types : 如果希望变量仅采用整数值或二进制值，请使用 integer=True 或 binary=True 的论点 new_variable 方法。或者，也可以调用 set_integer 和 set_binary 方法：研究方法。

Bounds : 如果希望变量只接受非负值，则可以在调用 new_variable 带着这样的论点 nonnegative=True 。如果要为变量设置不同的上下限，请添加约束或使用 set_min ， set_max 方法：研究方法。

基本线性规划

背包

这个 Knapsack 问题如下：给定同时具有权重和 usefulness ，我们希望装满容量受限的袋子，同时最大化袋子中所含物品的有用性(我们将考虑这些物品的有用性的总和)。出于本教程的目的，我们设置了袋子只能携带一定总重量的限制。

要实现这一点，我们必须关联到每个对象 o 在我们的收藏中 C 二元变量 taken[o] ，当对象在包中时设置为1，否则设置为0。我们正在努力解决以下MILP问题

\[\begin{split}\text{Max: } & \sum_{o \in L} \text{usefulness}_o \times \text{taken}_o\\ \text{Such that: } & \sum_{o \in L} \text{weight}_o \times \text{taken}_o \leq C\\\end{split}\]

使用Sage，我们将为我们的项目赋予随机权重：：

sage: C = 1

sage: L = ["pan", "book", "knife", "gourd", "flashlight"]

sage: L.extend(["random_stuff_" + str(i) for i in range(20)])

sage: weight = {}
sage: usefulness = {}

sage: set_random_seed(685474)
sage: for o in L:
....:     weight[o] = random()
....:     usefulness[o] = random()

现在我们可以定义MILP本身

sage: p = MixedIntegerLinearProgram()
sage: taken = p.new_variable(binary=True)

sage: p.add_constraint(p.sum(weight[o] * taken[o] for o in L) <= C)

sage: p.set_objective(p.sum(usefulness[o] * taken[o] for o in L))

sage: p.solve() # abs tol 1e-6
3.1502766806530307
sage: taken = p.get_values(taken)

找到的解决方案(当然)是可以接受的。

sage: sum(weight[o] * taken[o] for o in L)  # abs tol 1e-6
0.6964959796619171

我们要带手电筒吗？

sage: taken["flashlight"] # abs tol 1e-6
1.0

明智的建议。基于纯粹的随机考虑。

匹配

给出一张图 G ，匹配是一组成对不相交的边。空集是一个微不足道的匹配。因此，我们将注意力集中在最大匹配上：我们希望在图中找到基数为最大的匹配。计算图的最大匹配是一个多项式问题，这是Edmonds的一个著名结果。Edmonds的算法是基于局部改进的，并证明了如果给定的匹配不能被改进，则该匹配是最大的。在图论所能提供的那些算法中，该算法并不是最难实现的，尽管这个问题可以用非常简单的MILP来建模。

要做到这一点，我们需要--和前面一样--将一个二进制变量关联到我们的每个对象：图的边(值1表示对应的边包含在最大匹配中)。我们对边的限制是它们是不相交的，这就足够要求， x 和 y 作为两条边和 m_x, m_y 它们的关联变量，不平等 m_x + m_y leq 1 是满意的，因为我们确定他们两个不可能都属于匹配。因此，我们能够编写我们想要的MILP。然而，通过注意当且仅当两条边具有公共终点时，不能在匹配内同时获取两条边，就可以很容易地减少不等式的数量 v 。然后我们可以要求最多只有一条边入射到 v 被带到匹配的内部，这是一个线性约束。我们将解决以下问题：

\[\begin{split}\text{Max: } & \sum_{e \in E(G)} m_e\\ \text{Such that: } & \forall v, \sum_{\substack{e \in E(G) \\ v \sim e}} m_e \leq 1\end{split}\]

让我们编写这个MILP：：的SAGE代码

sage: g = graphs.PetersenGraph()
sage: p = MixedIntegerLinearProgram()
sage: matching = p.new_variable(binary=True)

sage: p.set_objective(p.sum(matching[e] for e in g.edges(sort=False, labels=False)))

sage: for v in g:
....:     p.add_constraint(p.sum(matching[e]
....:         for e in g.edges_incident(v, labels=False)) <= 1)

sage: p.solve()
5.0

sage: matching = p.get_values(matching, convert=bool, tolerance=1e-3)
sage: sorted(e for e, b in matching.items() if b)   # random
[(0, 4), (1, 6), (2, 3), (5, 8), (7, 9)]
sage: len(_)
5

流动

图论中的另一个基本算法：最大流！它由给定的一个有向图和两个顶点组成 s, t ，在发送最大 flow 从… s 至 t 使用的边缘 G 每一个都有一个最大的容量。

_images/lp_flot1.png

这个问题的定义几乎就是它的LP公式。我们正在寻找与每条边相关联的实际值，这些值将表示在两种类型的约束下流过它们的流的强度：

  • 到达顶点的流量(不同于 s 或 t )等于离开它的流量。

  • 通过一条边的流量受这条边的容量限制。

这就是说，我们必须最大化离开的流量 s ：所有这些都将最终落到 t ，因为其他顶点发送的数量与它们接收的数量相同。我们可以使用以下LP对流问题进行建模

\[\begin{split}\text{Max: } & \sum_{sv \in G} f_{sv}\\ \text{Such that: } & \forall v \in G, {\substack{v \neq s \\ v \neq t}}, \sum_{vu \in G} f_{vu} - \sum_{uv \in G} f_{uv} = 0\\ & \forall uv \in G, f_{uv} \leq 1\\\end{split}\]

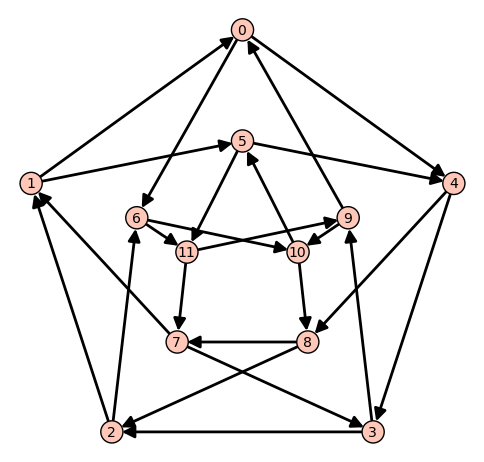
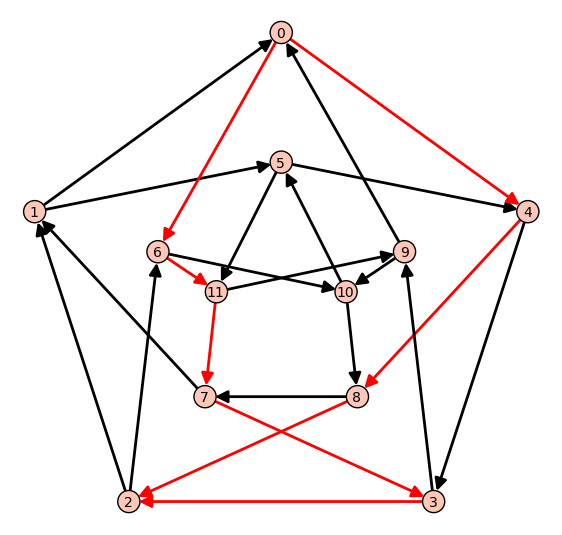
我们将解决Chvtal图的一个方向上的流问题，其中所有边的容量为1：：

sage: g = graphs.ChvatalGraph()
sage: g = g.minimum_outdegree_orientation()

sage: p = MixedIntegerLinearProgram()
sage: f = p.new_variable(real=True, nonnegative=True)
sage: s, t = 0, 2

sage: for v in g:
....:     if v != s and v != t:
....:         p.add_constraint(
....:             p.sum(f[v,u] for u in g.neighbors_out(v))
....:             - p.sum(f[u,v] for u in g.neighbors_in(v)) == 0)

sage: for e in g.edges(sort=False, labels=False):
....:     p.add_constraint(f[e] <= 1)

sage: p.set_objective(p.sum(f[s,u] for u in g.neighbors_out(s)))

sage: p.solve()  # rel tol 2e-11
2.0
_images/lp_flot2.png

解算器(后端)

Sage通过调用特定的库来解决线性规划问题。目前支持下列库：

  • CBC: 来自的求解器 COIN-OR 是在开放源码许可但与GPL不兼容的Eclipse公共许可(EPL)下提供的。可以使用Shell命令安装CBC和Sage CBC后端：：

    $ sage -i -c sage_numerical_backends_coin

  • CPLEX: 专利，但通过IBM的学术倡议免费提供给研究人员和学生。自.以来 :issue:`27790` ，仅支持12.8及更高版本。

    按照网站上的说明安装CPLEX，包括获取许可证密钥。

    然后找到ILOG CPLEX Studio安装的安装目录，其中包含子目录 cplex ， doc ， opl 等。设置环境变量 CPLEX_HOME 添加到此目录；例如，使用以下Shell命令(在MacOS上)：

    $ export CPLEX_HOME=/Applications/CPLEX_Studio1210

    或(在Linux上)：

    $ export CPLEX_HOME=/opt/ibm/ILOG/CPLEX_Studio1210

    现在验证您将在子目录中找到的CPLEX二进制文件 cplex/bin/ARCH-OS 正确启动，例如：：

    $ $CPLEX_HOME/cplex/bin/x86-64_osx/cplex
Welcome to IBM(R) ILOG(R) CPLEX(R) Interactive Optimizer...

    只需为以下步骤设置此环境变量：使用Shell命令安装Sage CPLEX后端：

    $ sage -i -c sage_numerical_backends_cplex

  • CVXOPT: 来自用于凸面优化的Python软件的LP求解器，使用内点法，总是安装在Sage中。

    在GPL下获得许可。

  • GLPK: A solver from GNU

    在GPLv3下获得许可。此解算器始终作为默认解算器安装在Sage中。

  • Gurobi: 专利，但通过Gurobi的学术项目免费提供给研究人员和学生。

    按照网站上的说明安装Gurobi，其中包括获取许可证密钥。安装应该使交互的GurobiShell gurobi.sh 在您的 PATH 。通过键入Shell命令来验证这一点 gurobi.sh **

    $ gurobi.sh
Python 3.7.4 (default, Aug 27 2019, 11:27:39)
...
Gurobi Interactive Shell (mac64), Version 9.0.0
Copyright (c) 2019, Gurobi Optimization, LLC
Type "help()" for help
gurobi>

    如果这不起作用，请调整您的 PATH 或创建符号链接，以便 gurobi.sh 已经找到了。

    现在使用Shell命令安装Sage Gurobi后端：：

    $ sage -i -c sage_numerical_backends_gurobi

  • PPL: 来自BugSeng的解算器。

    此解算器提供精确(任意精度)计算，始终安装在Sage中。

    在GPLv3下获得许可。