椭圆曲线¶
克雷莫纳数据库¶
克雷莫纳的椭圆曲线数据库是Sage的一部分。Sage标配了高达10,000条导体的曲线,还可以选择下载以访问他的完整表格。从Shell程序中,您应该运行::
sage -i database_cremona_ellcurve
自动下载并安装扩展表。
要使用数据库,只需通过以下方式创建一条曲线
sage: EllipticCurve('5077a1')
Elliptic Curve defined by y^2 + y = x^3 - 7*x + 6 over Rational Field
sage: C = CremonaDatabase()
sage: C[37]['allcurves']
{'a1': [[0, 0, 1, -1, 0], 1, 1],
'b1': [[0, 1, 1, -23, -50], 0, 3],
'b2': [[0, 1, 1, -1873, -31833], 0, 1],
'b3': [[0, 1, 1, -3, 1], 0, 3]}
sage: C.isogeny_class('37b')
[Elliptic Curve defined by y^2 + y = x^3 + x^2 - 23*x - 50
over Rational Field, ...]
还有一个Stein-Watkins数据库,其中包含数亿条椭圆曲线。不过,它的下载容量超过了2 GB!
布莱恩·伯奇的生日贺卡¶
布莱恩·伯奇最近参加了一次生日会议,我用塞奇绘制了他的生日贺卡的封面,列举了37岁以下所有最优的导体椭圆曲线,然后用粗大的随机色线绘制出来。正如您在下面看到的,绘制一条椭圆曲线就像调用它的Plot方法一样简单。此外,图形阵列命令允许我们轻松地将多个绘图合并到单个图形对象中。
sage: v = cremona_optimal_curves([11..37])
sage: w = [E.plot(thickness=10,rgbcolor=(random(),random(),random())) for E in v]
sage: graphics_array(w, 4, 5).show(axes=False)
绘制模数 \(p\)¶
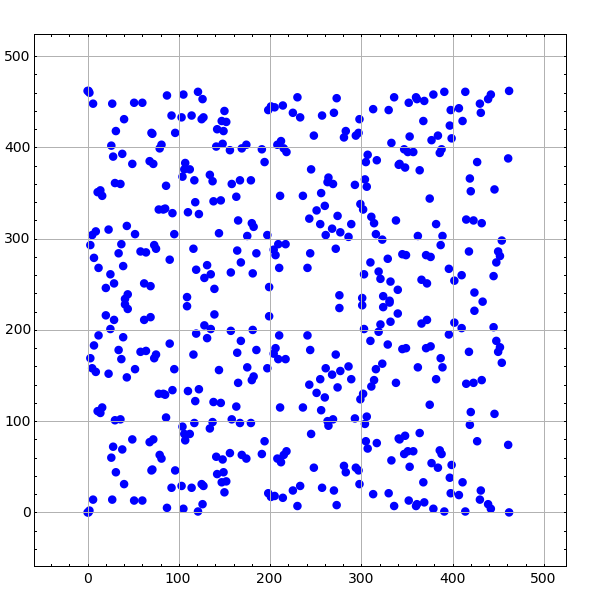
我们可以使用Sage的交互功能来绘制一条模为椭圆曲线的曲线图 \(p\) ,带有一个滑块,可以拖动它来更改质数 \(p\) 。Sage的交互功能对于交互更改参数和查看结果非常有用。类型交互?有关更多帮助和示例,请访问网页http://wiki.sagemath.org/interact.
在下面的代码中,我们首先定义椭圆曲线 \(E\) 使用克雷莫纳标签37a。然后我们定义了一个交互函数 \(f\) ,它是使用@InterAct Python修饰器进行交互的。因为默认情况下 \(p\) 是质数(2,500),Sage笔记本构建了一个滑块,它在质数上变化到 \(500\) 。当您拖动滑块并松开时,将绘制仿射图 \(\GF{p}\) 曲线上的点 \(E_{\GF{p}}\) 。当然,人们永远不应该在有限域上绘制曲线,这会使这变得更加有趣。
E = EllipticCurve('37a')
@interact
def f(p=primes(2,500)):
show(plot(E.change_ring(GF(p)),pointsize=30),
axes=False, frame=True, gridlines="automatic",
aspect_ratio=1, gridlinesstyle={'rgbcolor':(0.7,0.7,0.7)})
肖夫-埃尔基斯-阿特金点计数¶
Sage包括sea.gp,它是SEA(Schoff-Elkies-Atkin)算法的快速实现,用于计算椭圆曲线上的点数 \(\GF{p}\) 。
我们创建了有限域 \(k=\GF{p}\) ,在哪里 \(p\) 是下一个质数 \(10^{20}\) 。NEXT PRIME命令使用PARI的NextPRIME函数,但证明了结果的素性(与PARI不同,PARI只给出数字后面的下一个可能的素数)。Sage还具有下一个可能的质数函数。
sage: k = GF(next_prime(10^20))
计算它的基数,在幕后使用SEA。
sage: E = EllipticCurve_from_j(k.random_element())
sage: E.cardinality() # random, less than a second
99999999999371984255
要查看Sage如何选择何时使用SEA而不是其他方法,请键入E.Cardinality??并阅读源代码。在撰写本文时,它只是在任何时候使用SEA \(p>10^{18}\) 。
\(p\) -ADVAL监管机构¶
Sage拥有世界上最好的计算代码 \(p\) -椭圆曲线的随机调节器,这要归功于大卫·哈维和罗伯特·布拉德肖的工作。这个 \(p\) 椭圆曲线的二进调节子 \(E\) 在一个很好的普通素数 \(p\) 是全球经济的决定因素 \(p\) -Mordell-Weil群上的进向高度配对矩阵 \(E(\QQ)\) 。(这与当地或阿基米德的高度无关。)这是与Mazur-Tate-Teitelbaum中的调节器类似的 \(p\) --Birch和Swinnerton-Dyer猜想的模类。
特别是,Sage实现了Harvey对Mazur-Stein-Tate算法的改进,该算法建立在Kiran Kedlaya的Monsky-Washnitzer计算方法的基础上 \(p\) -二进上同调群。
我们建立了具有Cremona标号389a的椭圆曲线,它是最小导数和秩数的曲线 \(2\) 。然后我们计算这两个 \(5\) -ADDIC和 \(997\) -这条曲线的非常规监管机构。
sage: E = EllipticCurve('389a')
sage: E.padic_regulator(5, 10)
5^2 + 2*5^3 + 2*5^4 + 4*5^5 + 3*5^6 + 4*5^7 + 3*5^8 + 5^9 + O(5^11)
sage: E.padic_regulator(997, 10)
740*997^2 + 916*997^3 + 472*997^4 + 325*997^5 + 697*997^6
+ 642*997^7 + 68*997^8 + 860*997^9 + 884*997^10 + O(997^11)
在上面提到的新算法之前,即使计算一个 \(7\) -ADIC调节器至 \(3\) 精确的位数是一个不平凡的计算挑战。现在在Sage计算中 \(100003\) -ADY调节器是例行公事:
sage: E.padic_regulator(100003,5) # a couple of seconds
42582*100003^2 + 35250*100003^3 + 12790*100003^4 + 64078*100003^5 + O(100003^6)
\(p\) -ADDIC \(L\) -功能¶
\(p\) -ADDIC \(L\) -函数在椭圆曲线的算术研究中起着核心作用。他们是 \(p\) -复分析的进位类比 \(L\) -函数及其先导系数(在 \(0\) )是类似于 \(L^{(r)}(E,1)/\Omega_E\) 在 \(p\) --Birch和Swinnerton-Dyer猜想的模类。它们也出现在加藤、施奈德和其他人的定理中,这些定理证明了 \(p\) -使用岩泽理论的ADDIC BSD。
在《Sage》中的实现主要归功于我自己、克里斯蒂安·伍思里奇和罗伯特·波拉克的工作。我们使用Sage来计算 \(5\) -ADDIC \(L\) -阶数为389a的椭圆曲线的级数 \(2\) 。
sage: E = EllipticCurve('389a')
sage: L = E.padic_lseries(5)
sage: L
5-adic L-series of Elliptic Curve defined
by y^2 + y = x^3 + x^2 - 2*x over Rational Field
sage: L.series(3)
O(5^5) + O(5^2)*T + (4 + 4*5 + O(5^2))*T^2 +
(2 + 4*5 + O(5^2))*T^3 + (3 + O(5^2))*T^4 + O(T^5)
有界Shafarevich-Tate群¶
Sage实现了代码来计算椭圆曲线的Shafarevich-Tate群的许多显式界限。这一功能仅在Sage中可用,并使用结果Kolyvan in、Kato、Perrin-Riou等,以及伍思里奇和我的未发表论文。
sage: E = EllipticCurve('11a1')
sage: E.sha().bound() # so only 2 could divide sha
[2]
sage: E = EllipticCurve('37a1') # so only 2 could divide sha
sage: E.sha().bound()
([2], 1)
sage: E = EllipticCurve('389a1')
sage: E.sha().bound()
(0, 0)
这个 \((0,0)\) 在上面的最后一个输出中表明,Kolyvan in和Kato的Euler系统结果没有给出关于曲线的Shafarevich-Tate群的有限性的信息 \(E\) 。事实上,证明这种有限性是一个悬而未决的问题,因为 \(E\) 有名次 \(2\) ,并且其有限性仅对于椭圆曲线是已知的 \(L(E,1)\neq 0\) 或 \(L'(E,1)\neq 0\) 。
Kato,Schneider等人关于 \(p\) 详细说明:BSD猜想的ADDIC模拟生成边界的算法 \(p\) -Shafarevich-Tate集团的一部分。这些算法需要作为输入的显式计算 \(p\) -ADDIC \(L\) -功能、 \(p\) -ADIC调节器等,如Stein-Wu thrich中所解释。例如,下面我们使用Sage来证明 \(5\) 和 \(7\) 不要把我们这个级别的Shafarevich-Tate小组分开 \(2\) 曲线389a。
sage: E = EllipticCurve('389a1')
sage: sha = E.sha()
sage: sha.p_primary_bound(5) # iwasawa theory ==> 5 doesn't divide sha
0
sage: sha.p_primary_bound(7) # iwasawa theory ==> 7 doesn't divide sha
0
这与Birch和Swinnerton-Dyer猜想是一致的,该猜想预言Shafarevich-Tate群是平凡的。下面我们计算这个预测的顺序,它是浮点数 \(1.000000\) 达到一定的精确度。结果是一个浮点数,这有助于强调,证明Shafarevich-Tate群的猜想顺序通常甚至是有理数的问题是一个公开的问题!
sage: E.sha().an()
1.00000000000000
Mordell-Weil群与积分点¶
Sage既包括Cremona的mwrank库,也包括Simon的2下降GP脚本,用于计算椭圆曲线的Mordell-Weil组。
sage: E = EllipticCurve([1,2,5,17,159])
sage: E.conductor() # not in the Tables
10272987
sage: E.gens() # a few seconds
[(-3 : 9 : 1), (-3347/3249 : 1873597/185193 : 1)]
SAGE还可以计算扭子群、同源类、确定伽罗瓦表示的像、确定约简类型,并且包括在数域上的Tate算法的完整实现。
Sage拥有世界上计算椭圆曲线上所有整点的最快实现 \(\QQ\) ,由于克雷莫纳、迈克尔·马尔道斯和托拜厄斯·内格尔的工作。这也是唯一可用的免费开源实现。
sage: E = EllipticCurve([1,2,5,7,17])
sage: E.integral_points(both_signs=True)
[(1 : -9 : 1), (1 : 3 : 1)]
一个非常令人印象深刻的例子是最低阶导体椭圆曲线。 \(3\) ,它有36个整点。
sage: E = elliptic_curves.rank(3)[0]
sage: E.integral_points(both_signs=True) # less than 3 seconds
[(-3 : -1 : 1), (-3 : 0 : 1), (-2 : -4 : 1), (-2 : 3 : 1), ...(816 : -23310 : 1), (816 : 23309 : 1)]
计算所有整点的算法首先计算Mordell-Weil群,然后确定整点的边界,并列出满足这些边界的所有整点。有关完整的详细信息,请参阅科恩的新GTM 239。
复杂性在曲线的等级上呈指数级增长。我们可以进行上述计算,但使用已知的第一条等级曲线 \(4\) ,它在大约一分钟内完成(并输出64分)。
sage: E = elliptic_curves.rank(4)[0]
sage: E.integral_points(both_signs=True) # about a minute
[(-10 : 3 : 1), (-10 : 7 : 1), ...
(19405 : -2712802 : 1), (19405 : 2693397 : 1)]
\(L\) -功能¶
评估¶
接下来,我们用复合体进行计算 \(L\) -功能
的 \(E\) 。虽然上面的欧拉积只在右半平面上定义了一个解析函数,其中 \(\text{Re}(s) > 3/2\) ,Wiles等人的一个深层定理。(模性定理)意味着它具有对整个复平面和泛函方程的解析延拓。我们可以对函数进行评估 \(L\) 使用Sage在复杂平面上的任何位置(通过Tim Dokitser的代码)。
sage: E = EllipticCurve('389a1')
sage: L = E.lseries()
sage: L
Complex L-series of the Elliptic Curve defined by
y^2 + y = x^3 + x^2 - 2*x over Rational Field
sage: L(1) #random due to numerical noise
-1.04124792770327e-19
sage: L(1+I)
-0.638409938588039 + 0.715495239204667*I
sage: L(100)
1.00000000000000
泰勒级数¶
我们也可以计算泰勒级数 \(L\) 这要归功于蒂姆·多奇瑟的代码。
sage: E = EllipticCurve('389a1')
sage: L = E.lseries()
sage: Ld = L.dokchitser()
sage: Ld.taylor_series(1,4) #random due to numerical noise
-1.28158145691931e-23 + (7.26268290635587e-24)*z + 0.759316500288427*z^2 - 0.430302337583362*z^3 + O(z^4)
GRH¶
广义黎曼假设断言 \(L(E,s)\) 是以下形式的 \(1+iy\) 。Mike Rubinstein已经编写了一个C++程序,该程序是Sage的一部分,可以为任何 \(n\) 计算第一个 \(n\) 的价值 \(y\) 以至于 \(1+iy\) 是一个零 \(L(E,s)\) 。它还验证了关于这些零的黎曼假设(我认为)。鲁宾斯坦的程序也可以对一大类 \(L\) -函数,尽管并不是所有这些功能在Sage中都像在椭圆曲线上一样容易使用。下面我们计算第一个 \(10\) 的零点 \(L(E,s)\) ,在哪里 \(E\) 仍然是军衔 \(2\) 曲线389a。
sage: L.zeros(10)
[0.000000000, 0.000000000, 2.87609907, 4.41689608, 5.79340263,
6.98596665, 7.47490750, 8.63320525, 9.63307880, 10.3514333]