三维空间数据模型的研究现状

现有的三维空间数据模型可以分为：基于栅格结构的数据模型、
基于矢量结构的数据模型和混合结构数据模型。

1.基于栅格结构的数据模型

基于栅格结构的数据模型是二维栅格模型在三维空间的扩展，
它将三维空间划分为一系列连通但不重叠的几何体素。
构造栅格结构数据模型的方法主要有单元分解法、
空间枚举法、四面体格网法、K-单纯形剖分法等。

单元分解法通过定义一些相对规则的基本的几何形体
(如立方体、球、圆柱、矩形、菱形等)，
然后对基本对象进行布尔运算(交、并、差、积等)构造复杂对象。
用该类方法可以精确地定义几何形状，但难以表达拓扑关系。

空间枚举法采用单一形状的几何体来描述空间实体，
如立方体。这类方法的优点是可以对几何体建立空间索引，
从而提高空间搜索的效率，易于进行布尔运算和数据管理；
缺点是只能近似地描述空间实体，且占用的存储空间过大。
八叉树模型是基于空间枚举法的一种应用非常广泛的数据模型。
八叉树模型对三维空间的几何实体进行体元剖分，
每个体元具有相同的时间和空间复杂度；
通过对大小为2NX2NX2N三维对象进行递归分解，
最后构成一个具有根节点的方向图。如图1所示。
为了节省八叉树模型的存储空间，有学者对此进行了扩展，
提出利用线性八叉树模型进行压缩，
仅存储属于体对象的叶节点以及叶节点与根节点的关系。

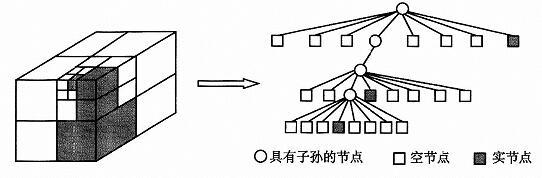
图1八叉树模型

四面体格网模型以不规则四面体作为描述空间实体的基本元素，
将任意一个三维空间实体剖分成一系列邻接但不重叠的四面体，
通过四面体间的邻接关系来反映空间实体间的拓扑关系，
如图2所示。其特点是能够根据三维空间采样点的坐标有效地实现插值运算、
几何和逻辑变换；但是该模型没有考虑空间实体的表面形态，

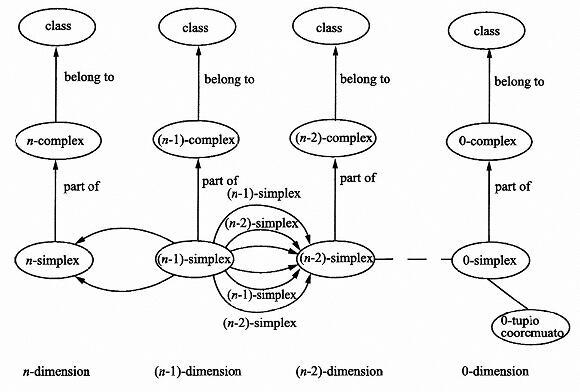
图2四面体格网模型

难于表达三维面状目标和线状目标，同时随描述精度的增加，
会需要大量的空间存储复杂的拓扑关系，整体数据量会急剧增大，
并且对空间实体的剖分算法仍存在一些问题有待解决。

K-单纯形剖分法扩展了四面体格网法，它以K单纯形作为基本元素，
将任意空间实体分解为与其维数相应的一系列单纯形，
从而解决了四面体格网模型只能对空间三维实体表达的问题，
可以将所有空间实体进行剖分表达。对空间实体的操作，
转化为对剖分后的单纯形集合的操作。
其缺陷在于由于对所有实体进行剖分而增加了操作的复杂度。

2.基于矢量结构的数据模型

基于矢量的数据模型以物体边界和表面为基础定义和描述空间实体。
构造矢量结构数据模型的方法主要有线框表示法、边界表示法、表面剖分法等。

线框表示法最早应用于计算机图形学和CAD/CAM领域，
它用一系列空间直线、圆弧和点来描述三维空间实体的外形，
在计算机内建立物体棱边起点和终点的线段表。
由于该表示法只有离散的空间线段，没有实在的面，
因此具有数据结构简单、数据存储量小、对硬件要求低、
易于掌握等特点。但它也存在所构成的图形含义不确切、
不能进行物体几何特性（体积、面积等）的量算、
不便于消除隐藏线、无法表示实体之间的拓扑关系等缺陷。

边界表示法基于空间实体的有限组成来描述几何对象，
即每个空间实体由有限个面组成，每个面由有限条边围成，
每条边由起点和终点定义。该方法直接给出了空间实体的边界描述，
有利于图形生成和几何特性的计算，
但难以精确表达带有曲面的空间实体，
缺乏对三维实体内部信息的描述。基于边界表示法，
荷兰学者Molennar提出了3DFDS模型，定义了结点、
弧段、边、面四种基本的几何元素以及基本元素与点、
线、面、体四种几何目标之间的拓扑关系，如图3所示。
3DFDS具有很强的表达拓扑关系和位置的能力，
但由于没有考虑空间实体的内部结构，
仅适于表达形状规则的简单空间实体，
难以表达没有规则边界的复杂实体。

在3DFDS的基础上，一些学者进行了扩展，发展了新的模型，
如SSM和V3D。其中SSM对3DFDS进行了一定的简化，
定义了两类基本的构造元素面、结点以及四类抽象的几何对象点、
线、面和体,并给出了点面、面线和面面之间拓扑关系的严格定义，
如图4.5所示。该模型去掉了3DFDS中的弧段元素，
结构更简单，有利于三维对象的可视化，
但同时却不利于复杂对象的构造。

V3D的特点在于在确定四类几何对象类型的基础上，
引入了DTM数据、影像数据和专题数据，
并把空间对象与各类信息结合起来，
因此在地表集合和属性信息的表达上更为强大，如图4.6所示。
其缺陷在于没有形成实体间拓扑关系的明确定义，
空间分析能力弱，同时地表对象与地形间的匹配也有待进一步完善。

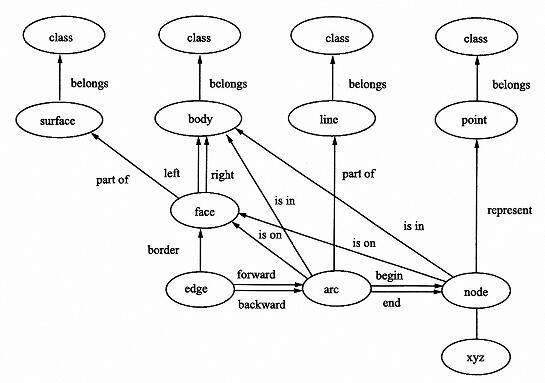
图3 3DFDS模型

表面剖分法将物体表面依据一定的算法分解为若干简单平面单纯形的集合，
将单纯形作为构建各种空间实体及描述拓扑关系的基本要素。
孙敏提出了基于三角形表面剖分的空间数据模型，
定义了点、线、面、体和DEM五类对象，
并将面分为曲面和折面两类，
通过对曲面和折面进行TIN三角形剖分实现对表面的表达和近似表达。

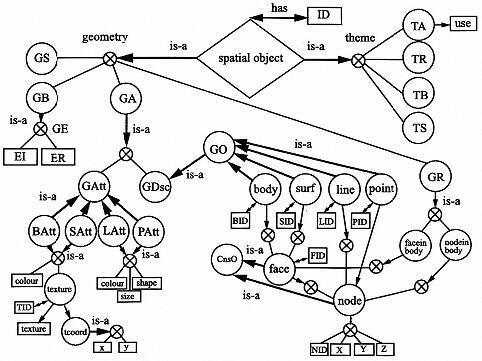
图4 V3D模型

虽然对体对象采用表面剖分进行表达可以减少不必要的数据冗余，
但剖分操作较为复杂，且难以控制剖分精度。

3.混合结构数据模型

为了集成栅格模型和矢量模型的优点，
一些学者将两种或两种以上的数据模型加以综合，
形成具有一体化结构的模型，即混合结构数据模型。
下面介绍几种比较具有代表性的该类数据模型。
Li Rong xing建立了一种多种数据模型集成的3DGIS系统，
采用BR和CSG描述规则对象，用TIN和八叉树描述不规则对象。
李清泉以八叉树和不规则四面体为基础提出了三维GIS的混合数据模型。
该模型以栅格结构的八叉树作为对象描述的总体框架，
控制对象空间的宏观分布；
以矢量结构的不规则四面体描述变化剧烈的局部区域，
较为精确地表达了细碎部分。
龚健雅针对矿山管理系统提出了面向对象的矢栅一体化数据模型，
定义了结点、弧段、断面、体元等13类空间对象，
用概括、联合、聚集来表达不同类之间的关系。李清泉、
李德仁提出了三种三维空间数据模型集成方法，
用于城市三维构模基于TIN和CSG的集成模型，用于地质、
海洋等领域的基于八叉树和四面体格网的混合模型，
具有一般性的矢量栅格集成的三维空间数据模型。
史文中基于面结构和体模型集成的思想提出了TIN结合
八叉树结构的混合数据模型，对于面结构用TIN表达用于可视化，
对体结构用八叉树进行构造，用于三维操作分析。

4.对比分析

上节讨论了目前国内外有关三维空间数据模型的研究进展，
综合分析比较，可以发现基于栅格结构的数据模型具有数据结构简单，
便于实现空间分析的优点；缺点是表达空间位置的几何精度低，
数据量大，三维图形输出效果较差；
基于矢量的数据模型具有三维模型描述精细、
图形输出美观等优点，但是对实体的整体及内部的描述能力较弱，
存在数据结构复杂、管理不方便等不足；
而基于混合结构的数据模型利用了不同数据模型
在表示不同空间实体时所具有的优点，
可以实现对三维空间现象有效完整的描述，
但同时也存在数据量大，必须在不同表示方法之间进行转换
以及如何保持转换的一致性的问题。

由于现实世界的复杂多样性，以及不同应用领域需要重点
表达的地理对象的差异性，导致了种类众多的三维空间数据模型。
这些模型有的侧重于空间分析，有的侧重于可视化，
有的侧重于拓扑关系的表达。就目前来看，
要实现一个完整的数据模型既能满足所有领域用户的需要、
又能完全的描述所有地理对象的性质是不可能的，
也是不现实的。就不同的应用领域，
根据研究对象及实现功能创建或使用不同的三维空间数据模型，
仍将是现在及以后很长一段时间内的主要解决方案。