numpy.random.RandomState.standard_cauchy

方法

RandomState.standard_cauchy(size=None)

从模式为0的标准柯西分布中提取样本。

也被称为洛伦兹分布。

参数:

size : int或int的元组，可选

输出形状。如果给定的形状是，例如， (m, n, k) 然后 m * n * k 取样。默认值为无，在这种情况下返回单个值。

返回:

样品 : ndarray或scalar

提取的样品。

笔记

全柯西分布的概率密度函数是

P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+ (\frac{x-x_0}{\gamma})^2 \bigr] }

标准柯西分布集 x_0=0 和 \gamma=1

柯西分布出现在被驱动谐振子问题的解中，也描述了谱线展宽。它还描述了以随机角度倾斜的线切割X轴时的值分布。

在研究假设正态性的假设检验时，观察检验是如何对柯西分布的数据进行的，这是它们对重尾分布敏感度的一个很好的指标，因为柯西分布看起来很像高斯分布，但尾部较重。

工具书类

[1]	NIST/Sematech E-统计方法手册，“柯西分布”，https://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm

[2]	柯西分布〉，摘自《数学世界——沃尔夫拉姆网络资源》。http://mathworld.wolfram.com/cauchydistribution.html

[3]	维基百科，“Cauchy发行版”https://en.wikipedia.org/wiki/Cauchy_发行版

实例

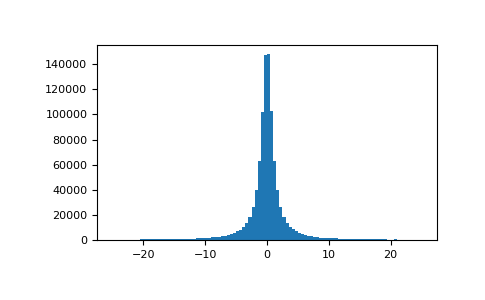
绘制样本并绘制分布图：

>>> import matplotlib.pyplot as plt
>>> s = np.random.standard_cauchy(1000000)
>>> s = s[(s>-25) & (s<25)]  # truncate distribution so it plots well
>>> plt.hist(s, bins=100)
>>> plt.show()