GDAL Grid 教程
网格化简介
网格化是从散乱的数据创建规则网格(或称之为栅格图像)的过程。通常,您在测量测量区域上有一组任意分散的网格,您希望将它们转换为常规网格,以便进一步处理并与其他网格组合。
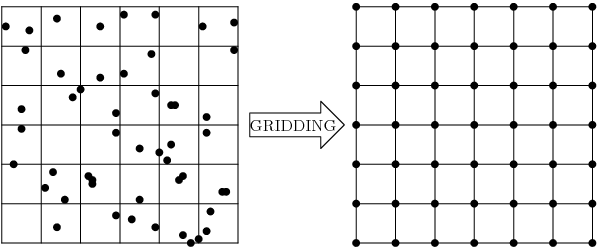
这个问题可以用数据插值或近似算法来解决。但是你不受插值的限制。有时您不需要插入数据,而是计算区域内的一些统计数据或数据度量。统计本身是有价值的,或者可以用来更好地选择插值算法和参数。
这就是GDAL Grid API的意义所在。它可以帮助您插入数据(请参见 Interpolation of the Scattered Data )或计算数据度量(请参见 Data Metrics Computation )
使用这个接口有两种方法。以编程方式通过 GDALGridCreate() C函数;对于最终用户 gdal_grid 公用事业。本文档的其余部分将讨论在GDAL Grid API中实现的算法及其参数的详细信息。
散乱数据的插值
逆距离
幂网格法的逆距离是加权平均插值。您应该为输入数组提供分散的数据值,包括每个数据点的坐标和输出网格几何图形。该函数将计算输出网格中给定位置的插值。
对于每个网格节点,结果值 \(Z\) 将使用以下公式计算:
在哪里?
\(Z_i\) 是一个已知值 \(i\) ,
\(r_i\) 是从网格节点到点的距离 \(i\) ,
\(p\) 是一种权势,
\(n\) 是指 Search Ellipse .
平滑参数 \(s\) 在欧几里德距离计算中用作相加项:
在哪里? \(r_{{ix}}\) 和 \(r_{{iy}}\) 是栅格节点到点之间的水平和垂直距离 \(i\) 分别。
在这种方法中,加权因子 \(w\) 是
见 GDALGridInverseDistanceToAPowerOptions 对于 GDALGridCreate() 参数和 投资分布 对于 gdal_grid 选项。
移动平均
移动平均是一种简单的数据平均算法。它使用椭圆形式的移动窗口来搜索值并平均窗口中的所有数据点。 Search Ellipse 可以按指定的角度旋转,椭圆的中心位于网格节点上。还可以设置要平均的最小数据点数,如果窗口中没有足够的点,网格节点将被视为空,并将用指定的NODATA值填充。
数学上可以用公式表示:
在哪里?
\(Z\) 是网格节点处的结果值,
\(Z_i\) 是一个已知值 \(i\) ,
\(n\) 是一些正在搜索的点 Search Ellipse .
见 GDALGridMovingAverageOptions 对于 GDALGridCreate() 参数和 平均的 对于 gdal_grid 选项。
最近的邻居
最近邻法不进行任何插值或平滑,它只取网格节点搜索椭圆中的最近点的值作为结果返回。如果找不到点,则返回指定的nodata值。
见 GDALGridNearestNeighborOptions 对于 GDALGridCreate() 参数和 最近的 对于 gdal_grid 选项。
数据度量计算
所有指标都有相同的控制选项集。见 GDALGridDataMetricsOptions .
最小数据值
在网格节点中找到最小值 Search Ellipse . 如果没有找到点,将返回指定的NODATA值。
在哪里?
\(Z\) 是网格节点处的结果值,
\(Z_i\) 是一个已知值 \(i\) ,
\(n\) 是指 Search Ellipse .
最大数据值
网格节点中找到的最大值 Search Ellipse . 如果没有找到点,将返回指定的NODATA值。
在哪里?
\(Z\) 是网格节点处的结果值,
\(Z_i\) 是一个已知值 \(i\) ,
\(n\) 是指 Search Ellipse .
数据范围
在网格中找到的最小值和最大值之间的差异 Search Ellipse . 如果没有找到点,将返回指定的NODATA值。
在哪里?
\(Z\) 是网格节点处的结果值,
\(Z_i\) 是一个已知值 \(i\) ,
\(n\) 是指 Search Ellipse .
搜索椭圆
网格算法中的搜索窗口,以旋转椭圆的形式指定。它由三个参数描述:
\(radius_1\) 是第一个半径 (\(x\) 如果旋转角度为0,则为轴,
\(radius_2\) 是第二个半径 (\(y\) 如果旋转角度为0,则为轴,
\(angle\) 是搜索椭圆旋转角度(逆时针旋转)。
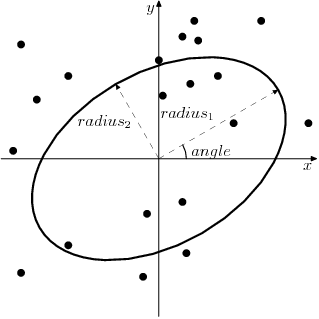
只有位于搜索椭圆(包括其边界线)内的点才能用于计算。