scipy.signal.windows.blackman

scipy.signal.windows.blackman(M, sym=True)

退回Blackman窗口。

布莱克曼窗是使用余弦和的前三项形成的锥形。它被设计成接近最小限度的泄漏。它接近最优，只比Kaiser窗口稍差一点。

参数

M集成

输出窗口中的点数。如果为零或更小，则返回空数组。

sym布尔值，可选

如果为True(默认值)，则生成对称窗口，用于过滤设计。如果为False，则生成周期性窗口，用于频谱分析。

退货

wndarray

最大值归一化为1的窗口(尽管在以下情况下不会显示值1 M 是均匀的，并且 sym 为True)。

注意事项

Blackman窗口定义为

\[W(N)=0.42-0.5\cos(2\pi n/M)+0.08\cos(4\pi n/M)\]

“精确布莱克曼”窗口的设计是为了消除第三和第四副瓣，但在边界处有不连续，导致6dB/OCT下降。“精确布莱克曼”窗口的设计是为了消除第三和第四副瓣，但在边界处有不连续性，导致6dB/OCT下降。该窗口是“精确”窗口的近似值，该窗口也不会使旁瓣归零，但在边缘处是平滑的，从而将衰减率提高到18dB/OCT。 [3]

对Blackman窗口的大多数引用来自于信号处理文献，在该文献中，它被用作许多用于平滑值的窗口函数之一。它也被称为变迹(意思是“去除脚部”，即平滑采样信号开始和结束处的不连续)或锥化函数。它被称为“近乎最优”的锥化函数，几乎和凯撒窗口一样好(以某些标准衡量)。

参考文献

1

布莱克曼，R.B.和图基，J.W.(1958)功率谱的测量，多佛出版，纽约。

2

Oppenheim，A.V.和R.W.Schafer离散时间信号处理。马鞍河上游，新泽西州：Prentice-Hall，1999，第468-471页。

3

放大图片创作者：Michael J.(1978年1月)。“论窗口在离散傅里叶变换谐波分析中的应用”。IEEE会议录66(1)：51-83 DOI:10.1109/PROC.1978.10837 。

示例

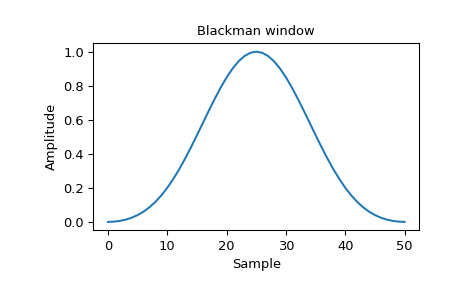
绘制窗口及其频率响应：

>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.windows.blackman(51)
>>> plt.plot(window)
>>> plt.title("Blackman window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

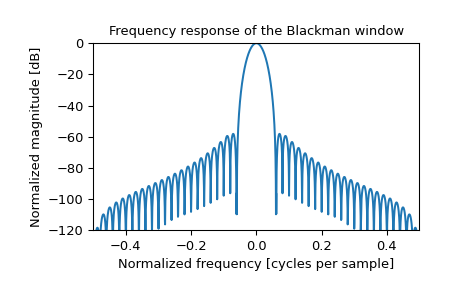
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = np.abs(fftshift(A / abs(A).max()))
>>> response = 20 * np.log10(np.maximum(response, 1e-10))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Blackman window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")