注解

此笔记本可在此处下载： Optimization_Tutorial.ipynb

优化教程（TD）

Rosenbrock函数

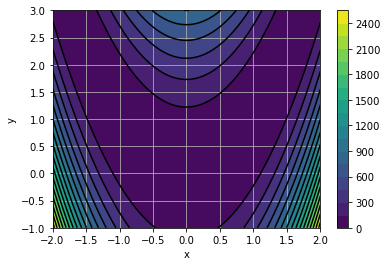
这个 Rosenbrock function 是优化算法的经典基准。其定义如下：

\[F（x，y）=（1-x）^2+100（y-x^2）^2\]

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def Rosen(X):
    """
    Rosenbrock function
    """
    x, y = X
    return (1-x)**2 + 100. * (y-x**2)**2


x = np.linspace(-2., 2., 100)
y = np.linspace(-1., 3., 100)
X, Y = np.meshgrid(x,y)
Z = Rosen( (X, Y) )

fig = plt.figure(0)
plt.clf()
plt.contourf(X, Y, Z, 20)
plt.colorbar()
plt.contour(X, Y, Z, 20, colors = "black")
plt.grid()
plt.xlabel("x")
plt.ylabel("y")
plt.show()

index=np.where(Z==Z.min())
print(index)
print(X[index])
print(Y[index])

(array([49]), array([74]))
[ 0.98989899]
[ 0.97979798]

问题

1. 使用蛮力求函数的最小值。评论函数评估的准确性和数量。

2. 与单纯形（Nelder Mead）算法相同的问题。

3. 尝试定位函数的两个最小值 \(x \mapsto x^4+3x^3y+6x^2y^2+3xy^3+y^4-4(x-y)(x+3y)\)

from scipy import optimize
X0 = [-1,-1] # Initial guess
sol = optimize.minimize(Rosen, X0, method = "nelder-mead")
sol

final_simplex: (array([[ 0.99999886,  0.99999542],
      [ 0.99996261,  0.99992484],
      [ 0.9999812 ,  0.99996926]]), array([  5.30934392e-10,   1.41212609e-09,   5.05898700e-09]))
          fun: 5.3093439186371615e-10
      message: 'Optimization terminated successfully.'
         nfev: 125
          nit: 67
       status: 0
      success: True
            x: array([ 0.99999886,  0.99999542])

曲线拟合

1. 选择数学函数 \(y = f(x, a, b)\) 然后编码。

2. 选择的目标值 \(a\) 和 \(b\) 您将尝试使用优化来查找。

3. 在网格上对其进行评估 \(x\) 价值观。

4. 在结果中添加一些噪波。

5. 查找 \(a\) 和 \(b\) 使用 curve_fit