注解

此笔记本可在此处下载： Optimization.ipynb

# Setup
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
params = {'font.size'     : 14,
          'figure.figsize':(10.0, 6.0),
          'lines.linewidth': 2.,
          'lines.markersize': 8,}
matplotlib.rcParams.update(params)

优化

范围

数学优化旨在通过最小化形式的函数来解决各种问题：

\[f（x）=e\]

哪里 \(f\) 如果 成本函数 ， \(X\) 是一种 \(N\) 参数的维向量和 \(e \in \mathscr R\) 。有关基本理论、解决方案的性质和实际考虑因素的更多信息可以找到：

• 论 Wikipedia ，

• 开（很好） Scipy lectures .

解决

Scipy 提供多种方法以解决其子包中的优化问题 优化

通用方法

scipy.optimize.minimize 允许使用多个通用优化算法。

from scipy import optimize

def f(X):
  """
  Cost function.
  """
  return (X**2).sum()

X0 = [1.,1.] # Initial guess
sol = optimize.minimize(f, X0, method = "nelder-mead")
X = sol.x
print "Solution: ", X

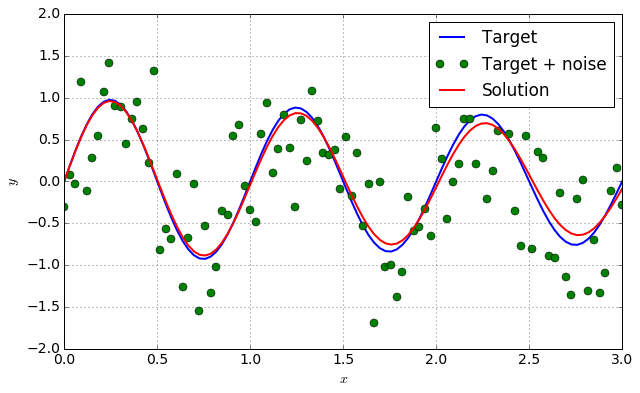
用最小二乘法拟合曲线

为了更方便地进行曲线拟合， scipy.optimize.curve_fit 可以使用。

def func(x, omega, tau):
    return np.exp(-x / tau) * np.sin(omega * x)


xdata = np.linspace(0, 3., 100)
y = func(xdata, omega = 2. * np.pi, tau = 10.)
ydata = y + .5 *  np.random.normal(size=len(xdata))

params, cov = optimize.curve_fit(func, xdata, ydata)
omega, tau  = params
ysol = func(xdata, omega, tau)


fig = plt.figure(0)
plt.clf()
plt.plot(xdata, y, label = "Target")
plt.plot(xdata, ydata, "o", label = "Target + noise")
plt.plot(xdata, ysol, label = "Solution")
plt.grid()
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.show()