欢迎来到Sage

这是对Sage作为计算器的简短介绍。

Sage命令行有一个提示符“sage：”。要试验以下示例，只需在提示后输入零件即可。

sage: 3 + 5
8

如果您在Jupyter笔记本上使用Sage，则同样将提示后的所有内容放入输入单元格中，然后按 Shift-Enter 以获得相应的输出。

插入符号的意思是“发扬光大”。

sage: 57.1^100
4.60904368661396e175

我们计算A的逆 \(2 \times 2\) 《智者》中的矩阵。

sage: matrix([[1, 2], [3, 4]])^(-1)
[  -2    1]
[ 3/2 -1/2]

这里我们集成了一个简单的函数。

sage: x = var('x')   # create a symbolic variable
sage: integrate(sqrt(x) * sqrt(1 + x), x)
1/4*((x + 1)^(3/2)/x^(3/2) + sqrt(x + 1)/sqrt(x))/((x + 1)^2/x^2 - 2*(x + 1)/x + 1)
- 1/8*log(sqrt(x + 1)/sqrt(x) + 1) + 1/8*log(sqrt(x + 1)/sqrt(x) - 1)

这就要求Sage解一个二次方程。这个符号 == 在Sage中代表平等。

sage: a = var('a')
sage: S = solve(x^2 + x == a, x); S
[x == -1/2*sqrt(4*a + 1) - 1/2, x == 1/2*sqrt(4*a + 1) - 1/2]

结果就是一系列等式。

sage: S[0].rhs()  # right hand side of the equation
-1/2*sqrt(4*a + 1) - 1/2

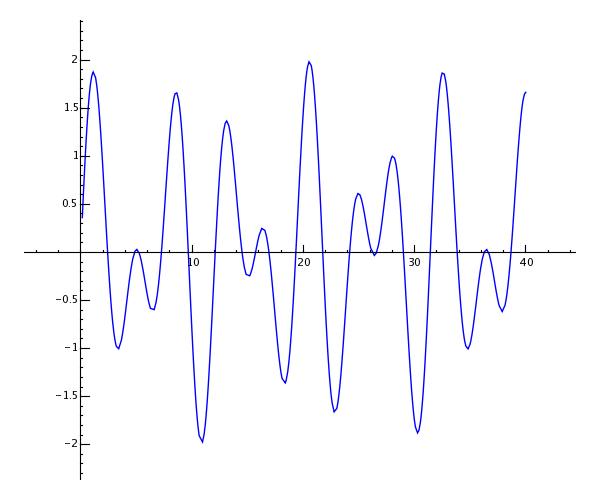
当然，Sage可以绘制各种有用的函数。

sage: show(plot(sin(x) + sin(1.6*x), 0, 40))
_images/sin_plot.png

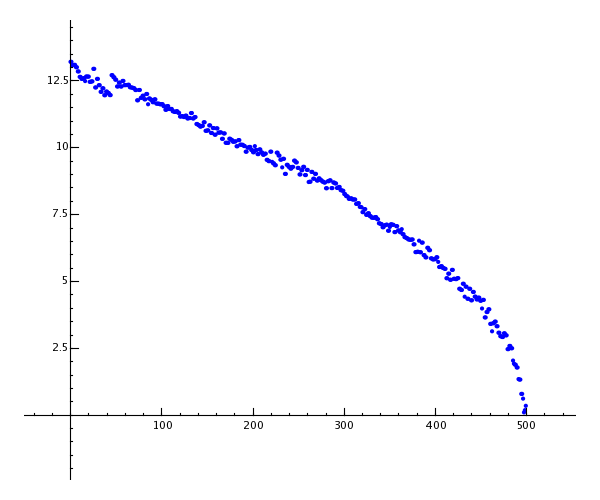
Sage是一个非常强大的计算器。为了体验它，我们首先创建一个 \(500 \times 500\) 随机数矩阵。

sage: m = random_matrix(RDF, 500)

Sage只需一秒钟就可以计算出矩阵的特征值并将其绘制成曲线图。

sage: e = m.eigenvalues()  # about 1 second
sage: w = [(i, abs(e[i])) for i in range(len(e))]
sage: show(points(w))
_images/eigen_plot.png

Sage可以处理非常大的数字，即使是数百万或数十亿位的数字。

sage: factorial(100)
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

sage: n = factorial(1000000)  # about 1 second
sage: len(n.digits())
5565709

这将计算至少100位的 \(\pi\) 。

sage: N(pi, digits=100)
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

这就要求Sage将一个多项式分解为两个变量。

sage: R.<x,y> = QQ[]
sage: F = factor(x^99 + y^99)
sage: F
(x + y) * (x^2 - x*y + y^2) * (x^6 - x^3*y^3 + y^6) *
(x^10 - x^9*y + x^8*y^2 - x^7*y^3 + x^6*y^4 - x^5*y^5 +
 x^4*y^6 - x^3*y^7 + x^2*y^8 - x*y^9 + y^10) *
(x^20 + x^19*y - x^17*y^3 - x^16*y^4 + x^14*y^6 + x^13*y^7 -
 x^11*y^9 - x^10*y^10 - x^9*y^11 + x^7*y^13 + x^6*y^14 -
 x^4*y^16 - x^3*y^17 + x*y^19 + y^20) * (x^60 + x^57*y^3 -
 x^51*y^9 - x^48*y^12 + x^42*y^18 + x^39*y^21 - x^33*y^27 -
 x^30*y^30 - x^27*y^33 + x^21*y^39 + x^18*y^42 - x^12*y^48 -
 x^9*y^51 + x^3*y^57 + y^60)
sage: F.expand()
x^99 + y^99

SAGE只需要不到1秒的时间来计算将1亿划分为正整数和的方法的数量。

sage: z = Partitions(10^8).cardinality()  # about .1 second
sage: z
1760517045946249141360373894679135204009...

Sage是世界上最先进的开源数学软件。