SAGE统计快速入门¶
这 Sage 快速入门教程是为MAA预备研讨会“SAGE:在本科生中使用开源数学软件”开发的(由美国国家科学基金会提供,截止日期0817071)。它是在知识共享署名-Share Alike 3.0许可证下授权的 (CC BY-SA )。
基本描述性统计¶
基本的统计函数最好是从 numpy 和 scipy.stats 。
例如,NumPy提供用于计算算术平均值和标准差的函数:
sage: import numpy as np
sage: np.mean([1, 2, 3, 5])
2.75
sage: np.std([1, 2, 2, 4, 5, 6, 8]) # rel to 1e-13
2.32992949004287
SciPy提供了更多的函数,例如计算调和平均值的函数:
sage: from scipy.stats import hmean
sage: hmean([1, 2, 2, 4, 5, 6, 8]) # rel to 1e-13
2.5531914893617023
我们不建议使用Python的内置 statistics 使用Sage的模块。它与Sage中定义的数字类型具有已知的不兼容性,请参见 :issue:`28234` 。
分配¶
让我们使用原生的Python随机生成器从给定类型的连续分布生成一个随机样本。
我们使用最简单的方法从(正态)均值为2的对数正态分布生成随机元素 \(\sigma=3\) 。
请注意,确实没有办法避免进行某种循环。
sage: my_data = [lognormvariate(2, 3) for i in range(10)]
sage: my_data # random
[13.189347821530054, 151.28229284782799, 0.071974845847761343, 202.62181449742425, 1.9677158880100207, 71.959830176932542, 21.054742855786007, 3.9235315623286406, 4129.9880239483346, 16.41063858663054]
我们可以检查数据的对数均值是否接近2。
sage: np.mean([log(item) for item in my_data]) # random
3.0769518857697618
下面是一个使用 Gnu scientific library 在引擎盖下。
让我们
dist是分配给标准差为3的连续高斯/正态分布的变量。然后,我们使用
.get_random_element()方法十次,每次加2,使平均值等于2。
sage: dist=RealDistribution('gaussian',3)
sage: my_data=[dist.get_random_element()+2 for _ in range(10)]
sage: my_data # random
[3.18196848067, -2.70878671264, 0.445500746768, 0.579932075555, -1.32546445128, 0.985799587162, 4.96649083229, -1.78785287243, -3.05866866979, 5.90786474822]
就目前而言,直接获取此类事物的直方图有点烦人。在这里,我们得到了这种分布的更大样本,并用10个柱状图绘制了一个直方图。
sage: my_data2 = [dist.get_random_element()+2 for _ in range(1000)]
sage: T = stats.TimeSeries(my_data)
sage: T.plot_histogram(normalize=False,bins=10)
Graphics object consisting of 10 graphics primitives
要访问离散分布,我们再次使用 Scipy 。
我们必须
import该模块scipy.stats。我们用
binom_dist表示具有20次试验和5%预期失败率的二项分布。这个
.pmf(x)方法给出的概率为 \(x\) 失败,然后我们将其绘制在条形图中 \(x\) 从0到20。(别忘了range(21)中的所有整数 zero to twenty 。)
sage: import scipy.stats
sage: binom_dist = scipy.stats.binom(20,.05)
sage: bar_chart([binom_dist.pmf(x) for x in range(21)])
Graphics object consisting of 1 graphics primitive
这个 bar_chart 函数执行直方图的一些职责。
Scipy的统计数据还可以做其他事情。在这里,我们找到了较早数据集的中位数(作为第50个百分位数)。
sage: scipy.stats.scoreatpercentile(my_data, 50) # random
0.51271641116183286
这里要记住的关键是查看文档!
从Sage内部使用R¶
这个 R project 是一个领先的统计分析软件包,在工业界和学术界广泛使用。
有几种访问R的方法;它们基于 rpy2 包裹。
最简单的方法之一就是把
r()围绕着你想要成为统计对象的东西,然后...通过以下方式使用R命令
r.method()将它们转交给Sage进行进一步处理。
下面的Kruskal-Wallis测试示例直接来自 r.kruskal_test? 在笔记本里。
sage: # optional - rpy2
sage: x = r([2.9, 3.0, 2.5, 2.6, 3.2]) # normal subjects
sage: y = r([3.8, 2.7, 4.0, 2.4]) # with obstructive airway disease
sage: z = r([2.8, 3.4, 3.7, 2.2, 2.0]) # with asbestosis
sage: a = r([x,y,z]) # make a long R vector of all the data
sage: b = r.factor(5*[1] + 4*[2] + 5*[3]) # create something for R to tell
....: # which subjects are which
sage: a; b # show them
[1] 2.9 3.0 2.5 2.6 3.2 3.8 2.7 4.0 2.4 2.8 3.4 3.7 2.2 2.0
[1] 1 1 1 1 1 2 2 2 2 3 3 3 3 3
Levels: 1 2 3
sage: r.kruskal_test(a,b) # do the KW test! # optional - rpy2
Kruskal-Wallis rank sum test
data: sage17 and sage33
Kruskal-Wallis chi-squared = 0.7714, df = 2, p-value = 0.68
看起来我们在这里不能拒绝零假设。
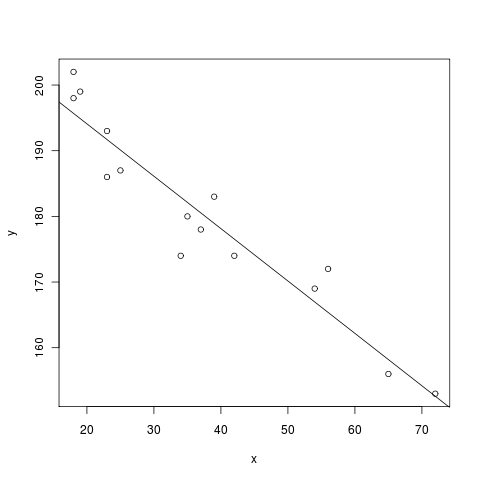
认真使用R的最好方法是使用所谓的“百分比指令”,简单地要求每个单独的单元格在R中完全求值。以下是John Verzani的线性回归示例 simpleR 文本。请注意,R还使用 # 用于指示注释的符号。
sage: %r # optional - rpy2
....: x = c(18,23,25,35,65,54,34,56,72,19,23,42,18,39,37) # ages of individuals
....: y = c(202,186,187,180,156,169,174,172,153,199,193,174,198,183,178) # maximum heart rate of each one
....: png() # turn on plotting
....: plot(x,y) # make a plot
....: lm(y ~ x) # do the linear regression
....: abline(lm(y ~ x)) # plot the regression line
....: dev.off() # turn off the device so it plots
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
210.0485 -0.7977
null device
1
要获取整个工作表以R进行计算(并能够忽略 % ),您也可以下拉 r 菜单中靠近顶部的选项,当前具有 sage 在里面。