图论和离散数学的SAGE快速入门

这 Sage 快速入门教程是为MAA预备研讨会“SAGE：在本科生中使用开源数学软件”开发的(由美国国家科学基金会提供，截止日期0817071)。它是在知识共享署名-Share Alike 3.0许可证下授权的 (CC BY-SA )。

由于计算机是离散的和有限的，离散数学中的主题自然易于实现和使用。我们将从图论开始。

图论

预定义的 graphs 对象提供了大量的示例。只需用标签来查看！

sage: graphs.[tab]

它的同伴 digraphs 也有许多内置的示例。

可视化图形类似于绘制函数。

sage: G = graphs.HeawoodGraph()
sage: plot(G)
Graphics object consisting of 36 graphics primitives

定义您自己的图表很容易。一种方法是如下所示。

• 在带有冒号的列表(回想一下编程教程中的概念)旁边放置一个顶点，以显示其相邻的顶点。例如，若要将顶点4放在顶点0和2的旁边，请使用 4:[0,2] 。

• 现在，将所有这些组合在大括号中(在编程教程的高级附录中，这称为 dictionary )。

sage: H=Graph({0:[1,2,3], 4:[0,2], 6:[1,2,3,4,5]})
sage: plot(H)
Graphics object consisting of 18 graphics primitives

邻接矩阵、其他图和类似的输入也被识别。

图中有顶点位置的“位置”信息。有几种不同的方法可以计算布局，也可以自己计算。预定义的图形通常带有“漂亮”的布局。

sage: H.set_pos(H.layout_circular())
sage: plot(H)
Graphics object consisting of 18 graphics primitives

顶点可以是很多东西，例如纠错码的码字。

备注

技术警告：它们需要是“不变的”，就像Python的元组一样。

这里我们有一个整数上的矩阵和一个作为顶点的变量矩阵。

sage: a=matrix([[1,2],[3,4]])
sage: var('x y z w')
(x, y, z, w)
sage: b=matrix([[x,y],[z,w]])
sage: a.set_immutable()
sage: b.set_immutable()
sage: K=DiGraph({a:[b]})
sage: show(K, vertex_size=800)

可以为边添加标签。

sage: L=graphs.CycleGraph(5)
sage: for edge in L.edges(sort=True):
....:     u = edge[0]
....:     v = edge[1]
....:     L.set_edge_label(u, v, u*v)
sage: plot(L, edge_labels=True)
Graphics object consisting of 16 graphics primitives

这与数学的其他领域有着天然的联系。这里我们计算立方体骨架的自同构群和本征值。

sage: C = graphs.CubeGraph(3)
sage: plot(C)
Graphics object consisting of 21 graphics primitives

sage: Aut=C.automorphism_group()
sage: print("Order of automorphism group: {}".format(Aut.order()))
Order of automorphism group:  48
sage: print("Group: \n{}".format(Aut)) # random
Group:
Permutation Group with generators [('010','100')('011','101'), ('001','010')('101','110'), ('000','001')('010','011')('100','101')('110','111')]

sage: C.spectrum()
[3, 1, 1, 1, -1, -1, -1, -3]

有大量的LaTeX支持图形。下图显示了可以执行的操作的示例；这是希伍德图。

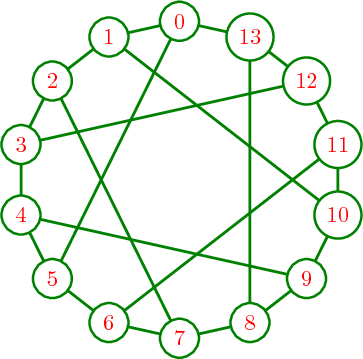
在下一个命令中按Tab键可查看所有可用选项。

sage: sage.graphs.graph_latex.GraphLatex.set_option?

更离散的数学

离散数学是一个广泛的领域，Sage对它的大部分都有很好的支持。这在很大程度上要归功于“Sage组合”这一群体。这些开发人员以前是为MuPad开发的(称为“Mupad组合”)，但在MuPad出售前不久切换到了Sage。

简单组合学

SAGE可以处理基本的组合结构，如组合和排列。

sage: pets = ['dog', 'cat', 'snake', 'spider']
sage: C=Combinations(pets)
sage: C.list()
[[], ['dog'], ['cat'], ['snake'], ['spider'], ['dog', 'cat'], ['dog', 'snake'], ['dog', 'spider'], ['cat', 'snake'], ['cat', 'spider'], ['snake', 'spider'], ['dog', 'cat', 'snake'], ['dog', 'cat', 'spider'], ['dog', 'snake', 'spider'], ['cat', 'snake', 'spider'], ['dog', 'cat', 'snake', 'spider']]

sage: for a, b in Combinations(pets, 2):
....:     print("The {} chases the {}.".format(a, b))
The dog chases the cat.
The dog chases the snake.
The dog chases the spider.
The cat chases the snake.
The cat chases the spider.
The snake chases the spider.

sage: for pair in Permutations(pets, 2):
....:     print(pair)
['dog', 'cat']
['dog', 'snake']
['dog', 'spider']
['cat', 'dog']
['cat', 'snake']
['cat', 'spider']
['snake', 'dog']
['snake', 'cat']
['snake', 'spider']
['spider', 'dog']
['spider', 'cat']
['spider', 'snake']

当然，我们经常想要这些数字，而且这些也是存在的。有些人很熟悉：

sage: Permutations(5).cardinality()
120

其他人则略有不同：

sage: D = Derangements([1,1,2,2,3,4,5])
sage: D.list()[:5]
[[2, 2, 1, 1, 4, 5, 3], [2, 2, 1, 1, 5, 3, 4], [2, 2, 1, 3, 1, 5, 4], [2, 2, 1, 3, 4, 5, 1], [2, 2, 1, 3, 5, 1, 4]]

还有一些更高级的，在这个例子中，是对称多项式。

sage: s = SymmetricFunctions(QQ).schur()
sage: a = s([2,1])
sage: a.expand(3)
x0^2*x1 + x0*x1^2 + x0^2*x2 + 2*x0*x1*x2 + x1^2*x2 + x0*x2^2 + x1*x2^2

与此相关的各种功能也可用。

sage: binomial(25,3)
2300

sage: multinomial(24,3,5)
589024800

sage: falling_factorial(10,4)
5040

你认得这个著名的身份吗？

sage: var('k,n')
(k, n)
sage: sum(binomial(n,k),k,0,n)
2^n

密码学(用于教育)

这一点也在 Number theory quickstart 。Sage有许多很好的密码学教学资源。

sage: # Two objects to make/use encryption scheme
sage: #
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: bin = BinaryStrings()
sage: #
sage: # Convert English to binary
sage: #
sage: P = bin.encoding("Encrypt this using S-DES!")
sage: print("Binary plaintext:  {}\n".format(P))
sage: #
sage: # Choose a random key
sage: #
sage: K = sdes.list_to_string(sdes.random_key())
sage: print("Random key:  {}\n".format(K))
sage: #
sage: # Encrypt with Simplified DES
sage: #
sage: C = sdes(P, K, algorithm="encrypt")
sage: print("Encrypted:  {}\n".format(C))
sage: #
sage: # Decrypt for the round-trip
sage: #
sage: plaintxt = sdes(C, K, algorithm="decrypt")
sage: print("Decrypted:  {}\n".format(plaintxt))
sage: #
sage: # Verify easily
sage: #
sage: print("Verify encryption/decryption: {}".format(P == plaintxt))
Binary plaintext:  01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001

Random key:  0100000011

Encrypted:  00100001100001010011000111000110010000011011101011111011100011011111101111110111110010101000010010001101101010101000010011001010100001010111000010001101000011001001111111110100001000010000110001011000

Decrypted:  01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001

Verify encryption/decryption:  True

编码理论

这里是一个简单的线性二进制码(组码)的例子。

从一个生成器矩阵开始 \(\ZZ/2\ZZ\) 。

sage: G = matrix(GF(2), [[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)

sage: C.is_self_dual()
False

sage: D = C.dual_code()
sage: D
[7, 3] linear code over GF(2)

sage: D.basis()
[
(1, 0, 1, 0, 1, 0, 1),
(0, 1, 1, 0, 0, 1, 1),
(0, 0, 0, 1, 1, 1, 1)
]

sage: D.permutation_automorphism_group()
Permutation Group with generators [(4,5)(6,7), (4,6)(5,7), (2,3)(6,7), (2,4)(3,5), (1,2)(5,6)]