描述

如果几何图形A和B在空间上重叠，则返回TRUE。如果两个几何图形具有相同的尺寸，每个几何图形至少有一个点不被另一个几何图形共享(或者等价地，两个几何图形都不覆盖另一个)，并且它们内部的交点具有相同的尺寸，则两个几何图形重叠。这种重叠关系是对称的。

	This function automatically includes a bounding box comparison that makes use of any spatial indexes that are available on the geometries. 要避免使用索引，请使用函数 _ST_Overlaps 。

由GEOS模块执行

	增强：已启用3.0.0支持 GEOMETRYCOLLECTION

注意：这是“允许的”版本，返回布尔值，而不是整数。

This method implements the OGC Simple Features Implementation Specification for SQL 1.1. S2.1.1.2//s2.1.13.3

This method implements the SQL/MM specification. SQL-MM 3：5.1.32

示例

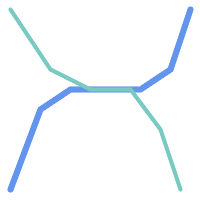
ST_Overlaps 退货 TRUE 在下列情况下：

MULTIPOINT / MULTIPOINT

LINESTRING / LINESTRING

POLYGON / POLYGON

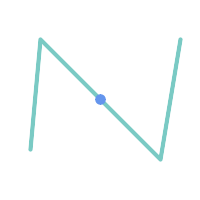
包含线串上的点，但由于它的尺寸较低，因此不会重叠或交叉。

SELECT ST_Overlaps(a,b) AS overlaps,       ST_Crosses(a,b) AS crosses,
       ST_Intersects(a, b) AS intersects,  ST_Contains(b,a) AS b_contains_a
FROM (SELECT ST_GeomFromText('POINT (100 100)') As a,
             ST_GeomFromText('LINESTRING (30 50, 40 160, 160 40, 180 160)')  AS b) AS t

overlaps | crosses | intersects | b_contains_a
---------+----------------------+--------------
f        | f       | t          | t

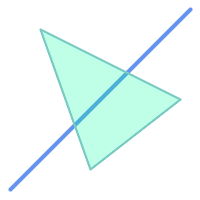
部分覆盖多边形的线串相交和交叉，但不重叠，因为它具有不同的标注。

SELECT ST_Overlaps(a,b) AS overlaps,        ST_Crosses(a,b) AS crosses,
       ST_Intersects(a, b) AS intersects,   ST_Contains(a,b) AS contains
FROM (SELECT ST_GeomFromText('POLYGON ((40 170, 90 30, 180 100, 40 170))') AS a,
             ST_GeomFromText('LINESTRING(10 10, 190 190)') AS b) AS t;

 overlap | crosses | intersects | contains
---------+---------+------------+--------------
 f       | t       | t          | f

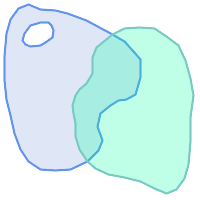
两个相交但都不包含在另一个中的多边形重叠，但不相交，因为它们的交点具有相同的尺寸。

SELECT ST_Overlaps(a,b) AS overlaps,       ST_Crosses(a,b) AS crosses,
       ST_Intersects(a, b) AS intersects,  ST_Contains(b, a) AS b_contains_a,
       ST_Dimension(a) AS dim_a, ST_Dimension(b) AS dim_b,
       ST_Dimension(ST_Intersection(a,b)) AS dim_int
FROM (SELECT ST_GeomFromText('POLYGON ((40 170, 90 30, 180 100, 40 170))') AS a,
             ST_GeomFromText('POLYGON ((110 180, 20 60, 130 90, 110 180))') AS b) As t;

 overlaps | crosses | intersects | b_contains_a | dim_a | dim_b | dim_int
----------+---------+------------+--------------+-------+-------+-----------
 t        | f       | t          | f            |     2 |     2 |       2

另请参阅

ST_Contains, ST_Crosses, ST_Dimension, ST_Intersects