拓扑空间关系

Topology—词来自于希腊文，它的原意是“形状的研究”。 拓扑特性指在拓扑变换（任意伸缩或变形，但不扭结或折叠） 下能够保持不变的几何属性。地理空间关系的研究所特別关注的 几个重要拓扑特性是连接性、包含和邻接性。

1.连接性。空间曲线的交点常称为结点。 连接性（connectivity）指曲线或弧段在结点处的相互联接关系。 在下图中，图a中的图形较大幅度地变形为图b所示， 但是曲线或弧段的连接关系并不变化，例如， 弧段1、2、3仍在结点4处连接；弧段2、5、6仍在结点B处连接。 可见，“连接性”是一种拓扑特性。

2.包含。包含（inclusion）关系有时仅就多边形或区域而言， 但我们这里采用更广泛的理解，将点、线、面之间能够定义的 所有包含关系或组成关系，都纳人包含的范畴。例如， 一个点在一条线上或是其端点个点在一个区域或多边形的边界上或内部； 一条线在一个多边形内部；一个区域在另一个区域的内部等。 比较上图之a和b图，可以证实这些空间关系在拓扑变换中皆保持不变。

位于一个较大区域内部的小区域，常称为“岛”。例如， 下图中，曲线4所围的小区域， 就是曲线2、3、6所联合包围的大区域中的一个“岛”。

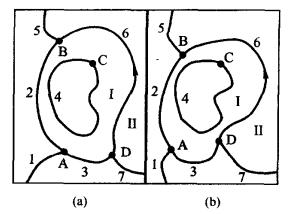
G1S中有两种基本组成关系值得注意。其一， 一条线可以者作由一连串点构成。如上述， 地理信息系统中的曲线，实际上是由很多足够小的线段组成的。 因此，计算机中只要给出一条曲线所有线段之结点的坐标系列， 就可以确定该曲线。其二，一个区域或一个多边形由若干条线围成， 这种情况也称为“多边形区域定义”。例如，在上图中， 曲线2、3、4和6围成了一个环状区域，它们定义了多边形I。 在拓扑变换中，尽管形状变化， 但这个环状区域由曲线2、3、4和6围成这一特性也是不变的。

邻接性。邻接性（contiguity）指共有公共边的两个区域的邻接关系， 如上图中，以曲线6为公共边的多边形I和n，就是相邻接的区域。 这种邻接性也不会因拓扑变换而改变。

如果给公共边指定方向，邻接性还可以进一步描述为“右邻”还是 “左邻”。例如，上图中，假定我们指定曲线6采取图中所示的方向， 那么，顺该方向看，多边形I就是左邻，或左多边形，多边形Ⅱ就是右邻， 或右多边形。如果曲线6的走向反转，那么，左邻与右邻关系也要颠倒过来。