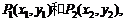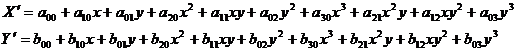7.2. 欧氏空间

定义7.2   设d为定义在集合Rⁿ上的距离函数，d: Rⁿ→R，对于Rⁿ中的任意元素x， y，x=(x₁， x₂， …， x_n)， y=(y₁， y₂， …， y_n)， 有d(x， y)= ， 则Eⁿ=(Rⁿ， d) 称为n维欧氏空间，Rⁿ的每个元素称为空间Eⁿ的点，d称为Rⁿ上的欧氏距离。当n=2时，E²称为欧氏平面。

欧氏空间是GIS中常用的一个重要数学空间，许多地理信息模型以欧氏空间为基础。下面讨论欧氏平面E²中的点、线、面的定义。

点：欧氏平面的点由一实数对(x， y)唯一确定，x， y 分别为其横坐标和纵坐标值。

通常也可以用矢量表示欧氏平面的点(x， y)， 即用从坐标原点到(x， y)的有方向的线段表示点(x， y)， 所有这些点的集合称为笛卡尔平面，记为R²。在笛卡尔平面中，允许下列对点的运算。

相加：(x₁， y₁)＋(x₂， y₂) = (x₁＋x₂， y₁＋y₂)

相减：(x₁， y₁)－(x₂， y₂) = (x₁－x₂， y₁－y₂)

乘常数：k(x， y) = (kx， ky)

求模：给定矢量a = (a₁， a₂)， 其模为 =

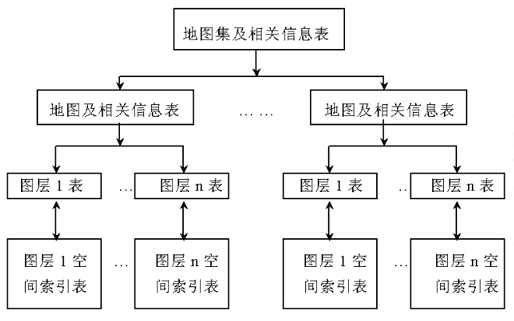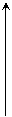
矢量间的距离：给定点a = (a₁， a₂)， b = (b₁，

b₂)， 从a到b的距离定义为 =

，即 =

矢量间的夹角 ：矢量a与b的夹角 由下列三角几何方程给定：

cos = (a₁b₁+ a₂b₂) / ( ・ )

矢量和的夹角 ：如图7-3所示， 在[0，360)范围内的值由下列三角几何方程唯一确定。

线：给定R²中两个不同点a和b，由a、b确定的线定义为点集 。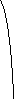

线段：给定R²中的两个不同点a和b，由a和b确定的线段定义为点集 。

图7-3  笛卡尔平面的矢量和

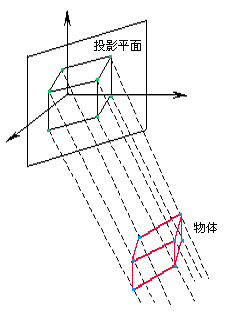
图7-4  线实体

    图7-4给出了上述定义的直观图示。由线的定义，我们可以得到多边形的定义。

多线段（Polyline）：R²上的多线段定义为线段（称为边）的有限集合，使得集合中边的端点除两个端点外（称为极点）任一端点恰好为两条边的端点。若任意两条边均不相交于端点外的任何地方，这类多线段称为简单多线段。若多线段中没有极点，则称该多线段是闭合的，如图7-5所示。

多边形：R²中由闭合多线段圈定的区域称为多边形，该多线段称为多边形的边界，多线段的每一端点称为多边形的节点。

简单多边形：若多边形的边界是简单多线段，则称为简单多边形。

凸多边形：若多边形的任一内角均小于180°，则称其为凸多边形。

凸多边形的一个重要性质是多边形内任意两点的边线仍落在多边形内。另一类较凸多边形条件弱一点的多边形称为星形多边形（Star-shaped Polygon）。在星形多边形中至少存在一个点，该点与多边形内其它任何点的连线均在多边形内，如图7-6所示。

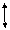
图7-5  多线段的类别

图7-6  多边形的类别

单调多线段点序列：欧氏平面上的点序列L = (p₁， p₂，…， p_n)，若存在欧氏平面上的一条直线l，使得将L上的点投影到l上时，L中的点的顺序不变。图7-7给出了单调和非单调点序列的实例。

单调多边形：一个多边形称为单调的，当且仅当其边界可以划分成两个多线段，并使得每一多线段的节点组成的序列都是单调的。

显然，凸多边形是单调多边形，但单调多边形不一定是凸多边形，单调多边形甚至不

图7-7  单调和非单调点序列

一定是星形多边形。图7-8给出的一个非星形多边形是单调多边形。

多边形的三角剖分：将多边形划分为若干个不相交的三角形。

对多边形作三角剖分时，可能需要在多边形区域内引入临时节点。不难证明，n个节点的多边形若在三角剖分时引入了m个临时节点，则形成的三角形数目一定为n+2m－2。若不需要引入临时节点，则三角剖分称为对角线三角剖分。

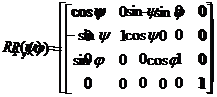
定理7.1 | 分，

则形成的三角形个数恰好为n－2。证明：对节点

个数n施归纳法。

当n=3时，恰有一个三角形，结论显见。

设n＜k时，定理成立。

当n=k时（k＞3），设多边形为P。沿着P的三角

剖分之一条边e（e不是多边形P的边）将P分割成两

个多边形P₁和P₂，因为节点数n＞3，这样的分割是可

                            行的。

 图7-8  一个非星形的单调多边形 设P₁有k₁个节点，P₂有k₂个节点，显然k₁+ k₂= k

                            + 2（P₁与P₂之公共边上的节点被重复计算），k₁＜k且k₂＜k。

由归纳假定，对于P₁和P₂定理成立。故P₁有k₁－2个三角形，P₂有k₂－2个三角形。则P的三角形数目为(k₁+ k₂－2)－2 =k－2。定理得证。

图7-9示了三角剖分的两种情形。读者可以自己验证上述公式。

图7-9  多边形的三角剖分

以上我们讨论了欧氏空间的一些几何对象及性质，这些几何对象都是GIS中的基本元素，由它们组成更为复杂的空间对象。

变换是一个重要的数学概念，在GIS中应用广泛。下面我们给出欧氏平面变换的概念及一些常见的变换类型。

变换：欧氏平面的任一函数f: R²→R²称为一个变换。

实际上，有用的变换一定保留了对象的某种性质，而改变了另外一些性质。下面是欧氏平面的一些常见变换。

欧氏变换：保留对象的大小和形状的变换。例如平移变换T，其数学形式为：对任意(x，y)∈R²，有：T(x，y)→(x+a， y+b)，这里a， b为常量。

相似变换：保留对象的形状，但大小可能发生变化的变换。

例如：缩放变换S₁(Scaling)是一类相似变换。其形式定义为：S₁是R²→R²的函数，对于任一(x，y)∈R²，有：S₁(x， y) = (ax， by)，这里a， b为常量。

仿射变换：保留对象仿射性质的变换。旋转变换R₁、反射变换R₂都是仿射变换。其定义如下：

R₁是R²→R²的函数，对任一(x， y)∈R²，有：

R₁(x， y) = (xcosθ－ysinθ， xsinθ + ycosθ)

这里θ是一个常数。R₁将欧氏平面的所有点以原点为中心，旋转了角度θ。

R₂是R²→R²的函数，对任一(x， y)∈R²， 有：

R₂(x， y) = (xcos2θ + ysin2θ， xsin2θ－ycos2θ)

这里θ是一个常数。R₂称为通过原点且与x轴夹角为θ的直线上的反射变换。

投影变换：保留对象投影性质的变换。投影变换的基本思想是在一个灯光源上将一幅图投影到一个屏幕。经过投影，一个圆可能变成一个椭圆。

拓扑变换：保留对象拓扑性质的变换。