9.3. DEM的表示方法¶
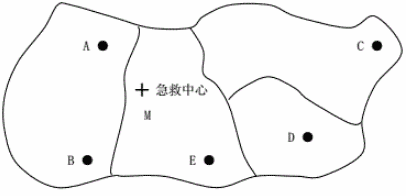
某地区地表高程的变化可用多种方法来模拟,用数学定义的表面或者点线影象都可用来表示DEM,如图9-2所示(据Mark1978年改编)。
图9-2 地表的表示方法
9.3.1. 数学方法¶
图9-3 分块法绘制的等高线图
数学方法拟合表面时需依靠连续三维函数,连续的三维函数能以高平滑度表示复杂表面。局部拟合法将复杂表面分成正方形象元,或面积大致相等的不规则形状的小块,而小块内的点观测值与表面匹配。尽管在小块的边缘,表面坡度不一定都是连续变化的,还是应使用加权函数来保证小块接边处的匹配。分块近似数学函数不太适合于制图,图9-3为分块法绘制的等高线图,其中可清晰地看出块间连续时漏掉了一些数据。但分块模拟广泛应用于复杂表面模拟的机助设计系统,已用于地下水、土壤特征或其它环境数据的表面内插。

9.3.2. 图形方法¶
1. 线模式――等高线
表示地形的最普通线模式是一系列描述高程测量曲线的等高线。剖面通常是坡度分析、正射影象制作和块状图生成等必须使用的派生产品。由于现有的地图大多数都绘有等高线,这些地图便是数字地面模型的现成数据源,用扫描仪在这些图上自动获取DEM数据方面已取得了很大进展。但数字化现有等高线产生的DEM比直接利用航空摄影测量方法产生的DEM数据质量差(Yoeli 1982)。而且数字等高线并不适合于坡度计算和制作晕渲地图,于是常将数字等高线转换成离散高程矩阵之类的点模式(见后面)。Ceruti(1980)和Yoeli(1984)阐述了将等高线内插成为高程矩阵的计算方法。Oswald和Raetzsch(1984)阐述了从一组表示等高线多边形产生高程矩阵的处理系统,此处所指的等高线是人工或栅格扫描仪数字化现有等高线加上谷底和山脊线组成的数字等高线。该系统就是有名的“格拉茨(Graz)地面模型”系统,该系统被认为是数字等高线转换成高程矩阵的现代化系统的代表。
格拉茨地面模型产生高程短阵的步骤是:将象元尺寸适合的格网复盖在包含山脊线、谷底线的等高线数字图象上,凡是位于或接近某一等高线的象元都将该等高线的高程值分配为这些象元的高程值,其它象元则分配-1。获得-1值的象元又按下述步骤分配高程值,即在栅格数据库的矩阵子集(或窗口)中进行内插。内插工作通常沿4条定向线搜索,即东西、南北、东南西北、东北西南等。内插时按已分配高程的象元高差的简单函数计算窗口内的局部最大坡度。然后将各窗口内的坡度分成4类,从最陡的一类开始给未分配高程的象元分配高程值。其它坡度类别重复相同的分配过程,而平坦地区是在所有DEM的非平坦部分都计算完后单独计算。Oswald和Raetzsch(1984)断定这种内插法──“依次最陡坡度算法”是完善而实用的技术。其他一些作者则持相反的观点(如Clarke等1982),他们认为非线性内插法“完全不令人满意”。
2. 点模式
(1)规则矩形格网――Grid
DEM最普通的形式是高程矩阵或规则矩形格网(GRID),高程数据直接由解析立体测图仪从立体航片上定量测量(Kelly等,1977)。高程矩阵还可由规则或不规则离散数据点内插产生。
由于计算机中矩阵的处理比较方便,特别是栅格为基础的地理信息系统中高程矩阵已成为DEM最通用的形式。英国和美国都用较粗略的矩阵(美国用63.5m象元格网)从全国1:25万地形图上产生了全国的高程矩阵,以1:5万或1:2.5万比例尺地图和航片为基础的分辨率更高的高矩阵正在这两个国家或其它国家扩大其使用范围。
虽然高程矩阵有利于计算等高线、坡度、坡向、山地阴影、自动描绘流域轮廓等,但规则的格网系统也有如下几方面的缺点:
① 在地形简单的地区存在大量冗余数据;
② 如不改变格网大小,无法适用于起伏复杂程度不同的地区;
③ 对于某些特种计算如视线计算时,过分依赖格网轴线。
先进采样法(Progressive Sampling)的实际应用很大程度上解决了采样过程中产生的冗余数据问题。先进采样法就是通过立体像对,根据视差模型自动选配左右影像的同名点建立数字高程模型。在产生DEM数据时,地形变化复杂的地区增加格网数(提高分辨率),而在地形起伏变化不大的地区则减少格网数(降低分辨率)。然而,数据存储中的冗余数据问题仍没有解决,因为连续变化的高度表面不太容易按照与栅格数据兼容的形式编码,而栅格数据又是专题制图需用的各种属性数据,当属性数据与地形数据组合使用时,它们的栅格大小必须统一,使DEM数据不得不填充所有的象元。
高程矩阵也和其它属性数据一样可能因栅格过于粗略而不能精确表示地形的关键特征,例如,山峰、洼坑、隘口、山脊、山谷线等。这些特征表示不正确时会给地貌分析带来一些问题。
不规则的离散采样点可以按两种方法产生高程矩阵:将规则格网覆盖在这些数据点的分布图上,然后用内插技术产生高程矩阵。当然,内插技术也可用来从一个粗略的高程矩阵产生更精细高程矩阵;把离散采样点作为点模式中不规则三角网系统的基础。
(2)不规则三角网(TIN―Triangulated Irregular Network)
① TIN特点
不规则三角网(TIN)是由Peuker和他的同事(1978)设计的一个系统,它是由不规则分布的数据点连成的三角网组成,三角面的形状和大小取决于不规则分布的观测点或称结点的密度和位置。不规则三角网与高程矩阵不同之处是能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置,因而能克服地形起伏不大的地区产生数据冗余的问题,利用它来绘制三维立体图具有较好的显示效果。对于某些类型运算比建立在数字等高线基础上的系统更有效。同时还能按地形特征点如山脊、山谷及其它重要地形特征获得DEM数据。不规则三角网方法能够较好地表示复杂地形,它的缺点是数据结构复杂,不便于规范化管理, 难以与矢量和栅格数据进行联合分析。而且,由于三角网是不规则排列的,计算每一点高程值的实时性不如规则网格模型。
TIN相当于是对采样点的一个平面三角剖分(如图9-4所示),因而它是一个连通平面图(黄力等,1999)。下面是计算N个点的任意一个平面三角剖分所含的三角形数和边数。设E表示边的数量,T表示三角形的数量。根据平面图中的欧拉公式有:
N - E+ T + 1= 2 (公式9-2)
由于同一条边为两个相邻三角形所共有,故
2*E= 3*T + Nh (公式9-3)
其中Nh是包围这N个点的凸壳上的点数。由上两式,我们可得到:
E= 3*(N - 1) - Nh; (公式9-4)
T = 2*(N - 1) - Nh; (公式9-5)
因此,可知对N个点的任何一个三角剖分,三角形的数量和边的数量是常量。
图9-4 不规则三角网
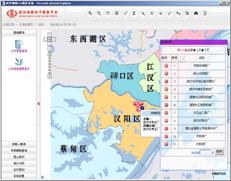
② TIN数据结构
用来描述TIN的基本元素有三个:结点、边和面。结点是相邻三角形的公共顶点,也是用来构建TIN的采样数据。边是两个三角形的公共边界,是TIN不光滑性的具体反映,它同时包含特征线、断裂线和区域边界。面是由最近的三个结点组成的三角形面,是TIN描述地形表面的基本单元,不能交叉和重叠。结点、边和面之间存在着关联、邻接等拓扑关系,类似于第二章定义的多边形网络完整的拓扑结构,但TIN没有考虑“洞”和“岛”的情形。TIN的表示方法有许多种,但是都比较复杂。图9-5是对应于图9-4的不规则三角网的一种表示方法,它包括点数据结构,边数据结构和三角形数据结构。
③ 狄洛尼(Delaunay)三角网
对于TIN模型,其基本要求有三点:
TIN是唯一的;
力求最佳的三角形几何形状,每个三角形尽量接近等边形状;
保证最邻近的点构成三角形,即三角形的边长之和最小。
图9-5 TIN的数据结构
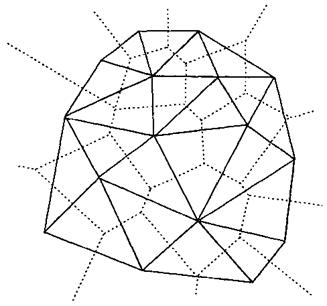
在所有可能的三角网中,狄洛尼(Delaunay)三角网在地形拟合方面表现最为出色,因此常常被用于TIN的生成。当不相交的断裂线等被作为预先定义的限制条件作用于TIN的生成当中时,则必须考虑带约束条件的Delaunay三角网。Delaunay三角网为相互邻接且互不重叠的三角形的集合,每一个三角形的外接圆内不包含其他的点。三角形外接圆内不包含其他点的特性被用作从一系列不重合的平面点建立狄洛尼三角网的基本法则,可称做空圆法则。Delaunay三角网是Voronoi图的对偶图,由对应Voronoi多边形共边的点连接而成。Delaunay三角形由三个相邻点连接而成,这三个相邻点对应Voronoi多边形有一个公共的顶点,此顶点同时也是狄洛尼三角形外接圆的圆心。图9-6描述了欧几里得平面上16个点的Delaunay三角网以及Voronoi图的对偶。
图9-6 16个平面点集的Delaunay三角网
④ Voronoi图及泰森多边形
Voronoi图又称为Dirichlet镶嵌( tessellation),其概念由Dirichlet 于1850 年首先提出;1907后俄国数学家Voronoi 对此作了进一步阐述,并提出高次方程化简;1911年荷兰气候学家A1H1Thiessen为提高大面积气象预报的准确度,应用Voronoi图对气象观测站进行了有效区域划分(吴立新,2003)。因此在二维空间中,Voronoi图也称为泰森(Thiessen)多边形。
设P = { p1 , p2 , …, pn } < R2 是二维欧式空间上的点集, d (・,・) 为欧式距离。称V ( pi ) = { p ∈R2 | d ( p , pi ) ≤d ( p , pj ) , i , j = 1 ,2 , …, n ,i ≠j}为Voronoi区域。简单地说,Voronoi 图是平面的一个划分,其控制点集P中任意两点都不共位,且任意四点不共圆,任意一个内点到该凸多边形的控制点pi的距离都小于该点到其他任何控制点pj 的距离(冯仲科,2006)。Voronoi 区域的边称为Voronoi 图的边,Voronoi 区域的顶点成为Voronoi 区域的顶点。Voronoi图如图9-6 虚线所示。因此,Voronoi图具有以下特性(华一新等,2001):
每个Voronoi 区域内仅含一个离散点数据;
每个Voronoi 区域内的点到相应离散点的距离最近;
位于Voronoi 区域边上的点到其两边的离散点的距离相等。
由于Delaunay三角网与Voronoi图的对偶关系。因此,在构造点集的Voronoi图之后,再对其做对偶图,即对每条Voronoi边(限有限长线段)做通过点集中某两点的垂线,便得到Delaunay三角网。同样,由Delaunay三角网也可以方便的得到与之对偶的Voronoi图。除了可以利用Delaunay三角网来求解Voronoi图以外,还有很多构造Voronoi图的方法,如半平面的交、增量构造方法、分而治之法等。
9.3.3. DEM三维表达方法¶
DEM的三维表达常用的包括立体等高线图、线框透视图、立体透视图以及各种地形模型与图像数据叠加而形成的地形景观等等。
1. 立体等高线模型
为了表示陆地和海底的地形高低起伏变化情况和形态特征,地形立体等高线表示法属于写景法,它将等高线作为空间直角坐标系中函数为Z=f(x,y)的空间图形投影到平面上所得到的立体效果,它在采用了三维坐标投影变换的同时,还需根据视线方向作隐线处理,以便使图形效果更富有立体感,如图9-7所示(许海涛,1999)。
2. 三维线框透视模型
线框透视图或线框模型(Wireframe)是计算机图形学和CAD/CAM领域中较早用来表示三维对象的模型,至今仍广为运用,流行的CAD软件、GIS软件等都支持三维对象的线框透视图建立。线框模型是三维对象的轮廓描述,用顶点和邻边来表示三维对象,其优点是结构简单、易于理解、数据量少、建模速度快,缺点是线框模型没有面和体的特征、表面轮廓线将随着视线方向的变化而变化、由于不是连续的几何信息因而不能明确地定义给定点与对象之间的关系(如点在形体内、外等),如图9-8所示。
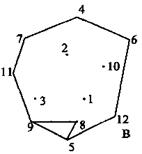
图9-8 DEM三维线框透视图
3. 地形三维表面模型
三维线框透视图是通过点和线来建立三维对象的立体模型,仅提供可视化效果而无法进行有关的分析。地形三维表面模型是在三维线框模型基础上,通过增加有关的面、表面特征、边的连接方向等信息,实现对三维表面的以面为基础的定义和描述,从而可满足面面求交、线面消除、明暗色彩图等应用的需求。简言之,三维表面模型是用有向边所围成的面域来定义形体表面,由面的集合来定义形体。
若把数字高程模型的每个单元看作是一个个面域,可实现地形表面的三维可视化表达,表达形式可以是不渲染的线框图,也可采用光照模型进行光照模拟,同时也可叠加各种地物信息,以及与遥感影像等数据叠加形成更加逼真的地形三维景观模型(图9-9)。