5.4. 空间数据的压缩与光滑

在空间数据输入计算机后，有时为了减少数据的存贮量节省存贮空间，加快后继处理速度，把大量的原始数据转换为有用的、有条理的、精炼而简单的信息的过程，这就称为数据简化或数据压缩。数据压缩的主要对象是线状要素中心轴线和面状要素边界数据。相反，在进行图形输出时，又需要将以前压缩的数据恢复成其原本来面目，必须对它们进行光滑，这称为曲线光滑。

5.4.1. 数据压缩

常用的数据压缩方法有如下几种。

  1. 间隔取点法

每隔k个点取一点，或每隔一规定的距离取一点，但首末点一定要保留。这种方法可大量压缩数字化使用连续方法获取的点和栅格数据矢量化而得到的点，但不一定能恰当地保留方向上曲率显著变化的点。

  1. 垂距法

这种方法是按垂距的限差选取符合或超过限差的点，其方法如图5-10所示。P2点的垂距大于限差，应保留；P3点的垂距小于限差，予以舍弃。

  1. 合并法（偏角法）

这个方法是沿着边界线，逐点计算通过当前点Pj的两条直线Lj1和Lj2之间的夹角αj，其中Lj1是经过Pj和Pj-k0两点的直线，而Lj2是经过Pj和Pj+k0这两点的直线。若｜αj｜小于某一阈值αo，那么就认为Pj是一应保留点。这个方法如图5-11所示。

image25

  1. 分裂法(道格拉斯－普克法)

这个方法可用以下几步来描述：

  1. 在给定的曲线的两端之间连一直线。

  2. 对曲线上每一点计算它与直线的垂直距离。若所有这些距离均小于某一阈值εo，那么就用它来表示原曲线。

  3. 若(2)中条件不满足，含有最大垂直距离的点Pj为保留点将原曲线分成两段曲线，对它们递归地重复使用分裂法。

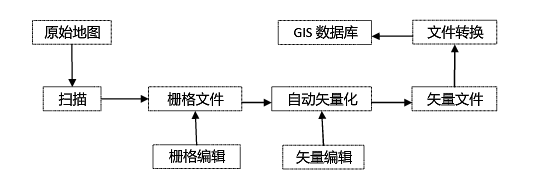
此法试图保持曲线走向和允许使用人员规定合理的限差，其执行过程如图5-12所示。

图中，实线为原曲线，虚线为压缩后的曲线。

image21 image22 image23 image24

(a)                 (b)                    (c)                 (d)

图 5-12 分裂法(道格拉斯－普克法)

5.4.2. 曲线光滑(曲线拟合)

曲线光滑是假想曲线(或接近它们的曲线)为一组离散点，寻找形式比较简单、性能良好的曲线解析式。曲线光滑有两种方式： 插值方式与逼近方式，前者所得到的曲线通过原先给定的离散点；而后者的曲线与所给的离散点相当“接近”。拉格朗日插值曲线（David F. Rogers，1981）和三次参数曲线是插值方式的曲线，贝齐尔曲线（Bezier）和B样条曲线是逼近方式的曲线。另外还有分段圆弧法、分段三次多项式插值法等方法（张宏，2006）。