2.3. 栅格数据结构¶
2.3.1. 栅格数据的基本概念¶
将工作区域的平面表象按一定分解力作行和列的规则划分,形成许多格网,每个网格单元称为像素,栅格数据结构实际上就是像元阵列,即像元按矩阵形式的集合,栅格中的每个像元是栅格数据中最基本的信息存储单元,其坐标位置可以用行号和列号确定。由于栅格数据是按一定规则排列的,所以表示的实体位置关系是隐含在行号、列号之中的。网格中每个元素的代码代表了实体的属性或属性的编码,根据所表示实体的表象信息差异,各像元可用不同的“灰度值”来表示。若每个像元规定N比特,则其灰度值范围可在0到2N—1之间;把白~灰色~黑的连续变化量化成8比特(bit),其灰度值范围就允许在0~255之间,共256级;若每个像元只规定1比特,则灰度值仅为0和1,这就是所谓二值图像,0代表背景,1代表前景。实体可分为点实体、线实体和面实体。点实体在栅格数据中表示为一个像元;线实体则表示为在一定方向上连接成串的相邻像元集合;面实体由聚集在一起的相邻像元集合表示。这种数据结构便于计算机对面状要素的处理。
用栅格数据表示的地表是不连续的,是量化和近似离散的数据,这意味着地表一定面积内(像元地面分辨率范围内)地理数据的近似性,例如平均值、主成分值或按某种规则在像元内提取的值等。另一方面,栅格数据的比例尺就是栅格大小与地表相应单元大小之比。像元大小相对于所表示的面积较大时,对长度、面积等的度量有较大影响。这种影响除对像元的取舍外,还与计算长度面积的方法有关。如图2-5(a)中a点与c点之间的距离是5个单位,但在图2-5(b)中,ac之间的距离可能是7,也可能是4,取决于算法。如以像元边线计算则为7,以像元为单位计算则为4。同样,图2-5(a)中三角形的面积为6个平方单位,而图2-5(b)中则为7个平方单位,这种误差随像元的增大而增加。
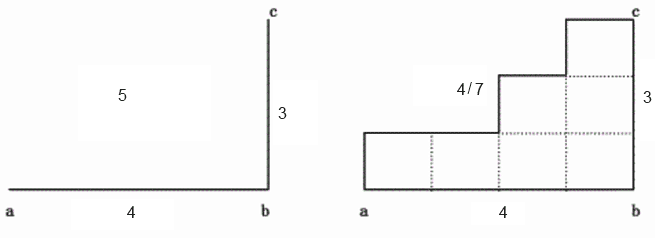
图2-5栅格数据结构对观测值的影响
2.3.2. 栅格数据层的概念¶
地理信息系统对现实世界的描述可以以地理空间位置为基础,按道路、行政区域、土地使用、土壤、房屋、地下管线、自然地形等不同专题属性来组织地理信息。在栅格数据结构中,物体的空间位置就用其在笛卡尔平面网格中的行号和列号坐标表示,物体的属性用像元的取值表示,每个像元在一个网格中只能取值一次,同一像元要表示多重属性的事物就要用多个笛卡尔平面网格,每个笛卡尔平面网格表示一种属性或同一属性的不同特征,这种平面称为层。地理数据在栅格数据结构中必须分层组织存储,每一层构成单一的属性数据层或专题信息层,例如同样以线性特征表示的地理要素,河流可以组织为一个层,道路可以作为另一层,同样以多边形特征表示的地理要素,湖泊可以作为一个层,房屋可以作为另一层,根据使用目的不同,可以确定需要建立哪些层及需要建立哪些描述性属性。在图2-6中,左图是现实世界按专题内容的分层表示,第三层为植被,第二层为土壤,第一层为地形,中间是现实世界各专题层所对应的栅格数据层,右图是对不同栅格数据层进行叠加分析得出的分析结论。
图2-6 栅格数据的分层与叠合
2.3.3. 栅格数据结构的表示¶
1. 二维数组
把栅格数据中各像素的值对应于二维数组相应的各元素加以存储的方式适合于灰度级大的浓淡图像的存储以及在通用计算机中的处理,所以是最常采用的一种方式。在采用二维数组的方式中,还有组合方式和比特面方式。
组合方式是在计算机的一个字长中存储多个像素的方式。从节约存储量的观点来考虑,经常在保存数据时采用。例如:16比特/字的计算机中,按每个像素8比特的数据对待的时候,如图2-7(a)所示,可以把相邻的两个像素数据分别存储到上8比特和下8比特中。同样,如果是按每个像素4比特数据,则一个字可以存储连续的4个像素的数据;如果是按每个像素1比特数据,则一个字可以存储16个像素的数据。
图2-7 组合方式和比特面方式
比特面方式,就是把数据存储到能按比特进行存取的二维数组(可以理解为1比特/1字)即比特面中的方式。对于n个比特的浓淡图像,如图2-7(b)所示,要准备n个比特面。在比特面k中(k=0,1,。。。,n-1),存储的是以二维形式排列着的各个像素值的第k比特(0或者1)的数据。另一方面,也有对于n比特/字的二维数组,把它作为n个比特面考虑,从而把二维图像存储到各比特面中的用法。以比特面作为单位进行处理时,其优点是能够在各面间进行高效率的逻辑运算,存储设备利用率高等,但也存在对浓淡图像的处理上耗费时间的问题。
2.一维数组
如果给栅格数据内的全体像素赋予按照某一顺序的一维的连续号码,则能够把栅格数据存储到一维数组中。上面的二维数组,在计算机内部如图2-8所示,实际上也变成为一维数组。
图2-8把栅格数据(二维数组)存储到一维数组中
其次,也有不是存储栅格数据全体,而只是把应该存储的像素的信息,按照一定规则存储到一维数组中去的方法。这种方法主要是在栅格数据中用来存储图形轮廓线信息等。具体来讲是坐标序列、链码等。
2.3.4. 栅格数据的组织方法¶
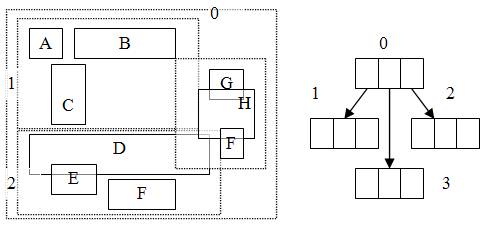
假定基于笛卡尔坐标系上的一系列叠置层的栅格地图文件已建立起来,那么如何在计算机内组织这些数据才能达到最优数据存取、最少的存储空间、最短处理过程呢?如果每一层中每一个像元在数据库中都是独立单元即数据值、像元和位置之间存在着一对一的关系,按上述要求组织数据的可能方式有三种(图2-9)。
1.以像元为记录的序列。不同层上同一像元位置上的各属性值表示为一个列数组(2-9a)。
2.以层为基础。每一层又以像元为序记录它的坐标和属性值,一层记录完后再记录第二层(图2-9b)。这种方法较为简单,但需要的存储空间最大。
3.以层为基础,但每一层内则以多边形(也称制图单元)为序记录多边形的属性值和充满多边形的各像元的坐标(图2-9c)。
这三种方法中1节省了许多存储空间,因为N层中实际只存储了一层的像元坐标;方法3则节省了许多用于存储属性的空间,同一属性的制图单元的n个像元只记录一次属性值。它实际上是地图分析软件包中所使用的分级结构,这种多像元对应一种属性值的多对一的关系,相当于把相同属性的像元排列在一起,使地图分析和制图处理较为方便;方法2则是每层每个像元一一记录,它的形式最为简单。
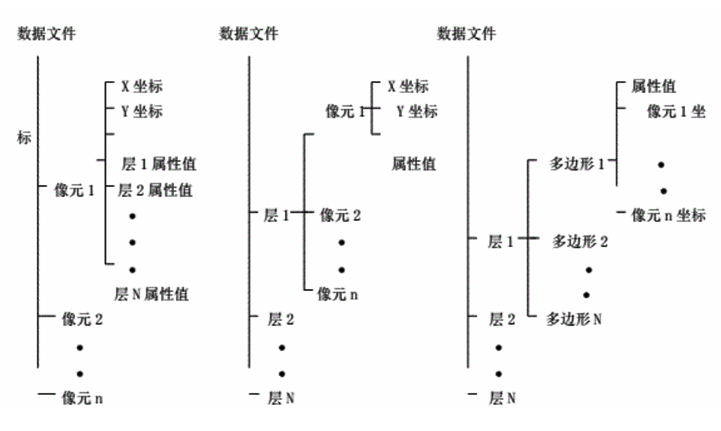
图2-9 栅格数据组织方式
2.3.5. 栅格数据取值方法¶
地图可以用来表示不同的专题属性,如何在地图上获取栅格数据,简单的方法是在专题地图上均匀地划分网格,或者将一张透明方格网叠置于地图上,每一网格覆盖部分的属性数据,即为该网格栅格数据的取值。但是常常会遇到一些特殊的情况,同一网格可能对应地图上多种专题属性,而每一个单元只允许取一个值,目前对于这种多重属性的网格,有不同的取值方法:
中心归属法:每个栅格单元的值以网格中心点对应的面域属性值来确定,如图2-10(a)所示。
长度占优法:每个栅格单元的值以网格中线(水平或垂直)的大部分长度所对应的面域的属性值来确定,如图2-10(b)所示。
面积占优法:每个栅格单元的值以在该网格单元中占据最大面积的属性值来确定,如图2-10(c)所示。
重要性法:根据栅格内不同地物的重要性程度,选取特别重要的空间实体决定对应的栅格单元值,如稀有金属矿产区,其所在区域尽管面积很小或不位于中心,也应采取保留的原则,如图2-10(d) 所示。
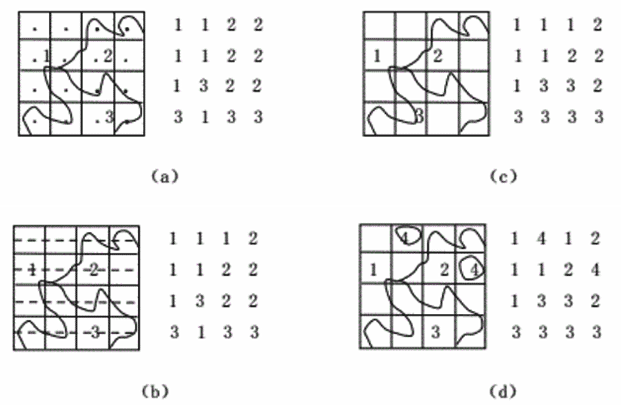
图2-10 栅格数据取值方法
2.3.6. 栅格数据存储的压缩编码¶
直接栅格编码是最简单最直观而又非常重要的一种栅格结构编码方法,通常称这种编码为图像文件或栅格文件。直接编码就是将栅格数据看作一个数据矩阵,逐行(或逐列)逐个记录代码,可以每行都从左到右逐像元记录,也可奇数据行从左到右,而偶数行由右向左记录,为了特定目的还可采用其它特殊的顺序。栅格结构不论采用何种压缩方法,其逻辑原型都是直接编码的网格文件。
当每个像元都有唯一一个属性值时,一层内的编码就需要m(行)×n(列)个存储单元。数字地面模型就属此种情况。如果一个多边形(或制图单元)内的每个像元都具有相同的属性值,就有可能大大节省栅格数据的存储需要量,关键是恰当地设计数据结构和编码方法。
1. 链式编码
链式编码又称为弗里曼链码(Freeman,1961)或边界链码。考虑图2-11中的多边形。该多边形边界可以表示为:由某一原点开始并按某些基本方向确定的单位矢量链。基本方向可定义为:东=0,南=3,西=2,北=1等。如果再确定原点为像元(10,1),则该多边形界按顺时方向的链式编码为:
0,1,02,3,02,1,0,3,0,1,03,32,2,33,02,1,05,32,22,3,23,3,23,1,22,1,22,1,22,1,22,13
链式编码对多边形的表示具有很强的数据压缩能力,且具有一定的运算功能,如面积和周长计算等,探测边界急弯和凹进部分等都比较容易。但是,叠置运算如组合、相交等则很难实施,除非还原成栅格结构方可,况且公共边界需要存储两次,从而产生多余的数据。
2. 行程编码
只在各行(或列)数据的代码发生变化时依次记录该代码以及相同代码重复的个数,即按(属性值,重复个数)编码,图2-12可沿行方向进行行程编码:
1行:(3,3),(4,5); 2行:(3,4),(4,4); 3行:(1,1),(3,3),(4,3),(2,1);4行:(1,2),(3,3),(2,3);5行:(1,4),(3,1),(2,3); 6行:(1,4),(2,4); 7行:(1,5),(2,3); 8行:(1,5),(2,3)。
逐个记录各行(或列)代码发生变化的位置和相应的代码,即按(位置,属性值)编码,图2-12可沿列方向进行行程编码:
1列:(1,3),(3,1); 2列:(1,3),(4,1); 3列:(1,3),(5,1);4列:(1,4),(2,3),(5,1); 5列:(1,4),(4,3),(6,2),(7,1);6列:(1,4),(4,2);7列:(1,4),(4,2);8列:(1,4),(3,2)。
按行(或列)记录相同代码的始末像元的列号(或行号)和相应的代码,即按(起位,止位,属性值)编码,图2-12可沿行方向进行程编码:
1行:(1,3,3),(4,8,4);2行:(3,4,3),(5,8,4); 3行:(1,1,1),(2,4,3),(5,7,4),(8,8,2); 4行:(1,2,1),(3,5,3),(6,8,2);5行:(1,4,1),(5,5,3),(6,8,2);6行:(1,4,1),(5,8,2);7行:(1,5,1),(6,8,2);8行:(1,5,1),(6,8,2)。
图2-11 栅格地图上的一个简单区域
空间数据库
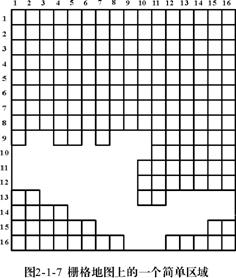
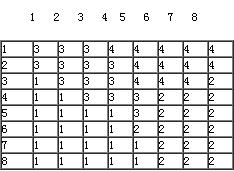
图2-12多区域栅格地图
3. 块式编码
块式编码是将行程编码扩大到二维的情况,把多边形范围划分成由像元组成的正方形,然后对各个正方形进行编码。块式编码数据结构中包括3个数字:块的原点坐标(可以是块的中心或块的左下角像元的行、列号)和块的大小(块包括的像元数),再加上记录单元的代码组成。图2-13说明如何对图2-12所示栅格地图进行分块,其块式编码如下:
(1,1,2,3),(1,3,1,3),(1,5,3,4),(1,8,1,4),(2,3,1,3),(2,4,1,3),(2,8,1,4),(3,1,1,1),(3,2,1,3),(3,3,2,3),(3,8,1,2),(4,1,1,1),(4,2,1,1),(4,5,1,3),(4,6,1,2),(4,7,2,2),(5,1,4,1),(5,5,1,3),(5,6,1,2),(6,5,1,2),(6,6,3,2),(7,5,1,1),(8,5,1,1)。
一个多边形所能包含的正方形越大,多边形的边界越简单,块式编码的效果就越好。行程和块式编码都对大而简单的多边形更有效,而对那些碎部仅比像元大几倍的复杂多边形效果并不好。 块式编码即中轴变换的优点是多边形之间求并及求交都方便;探测多边形的延伸特征也较容易。但对某些运算不适应,必须再转换成简单栅格数据形式才能顺利进行。
3 |
3 |
3 |
4 |
4 |
4 |
4 |
4 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
4 |
1 |
3 |
3 |
3 |
4 |
4 |
4 |
2 |
1 |
1 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
图2-13 块式编码分解示意图
图2-14四叉树分解过程

图2-15 四叉树结构
4. 四叉树编码
将图像区域按四个大小相同的象限四等分,每个象限又可根据一定规则判断是否继续等分为次一层的四个象限,无论分割到哪一层象限,只要子象限上仅含一种属性代码或符合既定要求的少数几种属性时,则停止继续分割。否则就一直分割到单个像元为止。这种分块过程如图2-14所示。而块状结构则用四叉树来描述,如图2-15所示。按照象限递归分割的原则所分图像区域的栅格阵列应为2n×2n(n为分割的层数)的形式。
所谓四叉树结构,即把整个2n×2n像元组成的阵列当作树的根结点,树的高度为n级(最多为n级)。每个结点有分别代表南西(SW)、南东(SE)、北西(NW)、北东(NE)四个象限的四个分支。四个分支中要么是树叶,要么是树叉。树叶不能继续划分,说明该四分之一范围或全属多边形范围或全不属多边形范围,该结点代表子象限具有单一的代码;树叉不只包含一种代码,说明该四分之一范围内,部分在多边形内,另一部分在多边形外,因而必须继续划分,直到变成树叶为止。四叉树编码有指针四叉树编码和线性四叉树编码两种方法。
(1)指针四叉树
指针四叉树编码是通过在子结点与父结点之间设立指针的方式建立起整个结构。按这种方式,四叉树的每个结点通常存储6个量,即四个子结点指针、一个父结点指针和该结点的属性代码。这种方法除了要记录叶结点外,还要记录中间结点,一般要占用较大存储空间。
(2)线性四叉树
线性四叉树编码为美国马里兰大学地理信息系统中采用的编码方法,它的基本思想是:不需记录中间结点和使用指针,仅记录叶结点,并用地址码(如Morton码等)表示叶结点的位置。因此,其编码包括叶结点的地址码和本结点的属性或灰度值,并且地址码隐含了叶结点的位置和深度信息。最常见的地址码是四进制或十进制Morton码。
①基于深度和层次的线性四叉树编码
该编码记录每个终止结点(或叶结点)的地址和值,值就是子区的属性代码,其中地址包括两部分,共32位(二进制),最右边4位记录该叶结点的深度,即处于四叉树的第几层上,有了深度可以推知子区大小;左边的28位记录路径,从右边第五位往左记录从叶结点到根结点的路径,0,1,2,3分别表示SW、SE、NW、NE。如图2-16表示的第4个结点深度为3,第一层处于SE象限,第二层处于SW象限,第三层处于NW象限。表示为二进制为:
 28位 4位
28位 4位
0 0 0 0 … … 0 0 0 1 0 0 1 0 0 0 1 1
 (路径1SE,0SW,2NW) 1 0 2 深度3
(路径1SE,0SW,2NW) 1 0 2 深度3
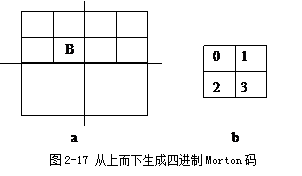
图2-16基于深度和层次的线性四叉树编码的示意图
每层象限位置由二位二进制数表示,共6位,记录了各个叶子的地址,再记录相应代码值,就记录了整个图像。
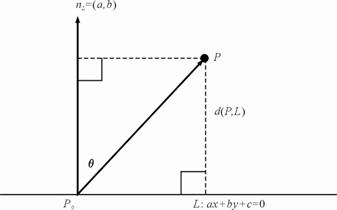
②四进制地址码
该编码方法是从整体开始水平和垂直分隔,每分隔一次,增加一位数字。如图2-17(b)为对图2-17(a)进行第一次分隔后得到四个区域(0,1,2,3),即每一个位均是用一个小于4的四进制数来表示位置。因此,该码的位数表示分隔的次数。进行第二次分隔后得到“B”的地址编码为“03”。
②十进制地址码(Morton码)
Morton码是这样的:给出2个数,把它们的二进制位隔个放置,比如对于3和4,
( 0 0 0 0 0 0 1 1 )2 = (3)10,
( 0 0 0 0 0 1 0 0 )2 = (4)10,
则它们的Morton码是(0000 0000 0010 0101)2 = (37)10。第一个数的第i位对应Morton码的第(2*i-1)位,第二个数的第j位对应Morton码的第(2*j)位。其中,i和j从1开始。
在一个n×n的图像阵列中,每个像元点都相应的给出一个Morton码。如图2-18为8×8的图像阵列每一像元的Morton码。如第7列5行的Morton码为55,即(7)10=(0111)2,(5)10=(0101)2,两二进制交换位后为(00110111)2=(55)10。

图2-18 8×8的图像阵列每一像元的Morton码值
这样就可将用行列表示的二维图像,用Morton码写成一维数据,通过Morton码就可知道象元的位置(臧淑英,2003)。
把一幅2n×2n的图像压缩成线性四叉树的过程为:
●按Morton码把图象读入一维数组;
●相邻的四个象元比较,一致的合并,只记录第一个象元的Morton码;
●比较所形成的大块,相同的再合并,直到不能合并为止。
对用上述线性四叉树的编码方法所形成的数据还可进一步用游程长度编码压缩。压缩时只记录第一个象元的Morton码。
如对于图2-20为图2-19所示图像的Morton。该栅格图像的压缩处理过程为:
图2-19 4×4的图像阵列

图2-20 4×4的图像阵列对应的Morton码
●按Morton码读入一维数组;
Morton码:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
象 元 值: A A A B A B B B A A A A B B B B
●四相邻象元合并,只记录第一个象元的Morton码。由于Morton码8,9,10,11的像元均为A,故只记录第一个Morton码8即可,从而达到压缩的目的;
0 1 2 3 4 5 6 7 8 12
A A A B A A B B A B
●由于不能进一步合并,则可用行程长度编码压缩。
0 3 4 6 8 12
A B A B A B
在解码时,根据Morton码就可知道象元在图像中的位置(左上角),本Morton码和下一个Morton码之差即为象元个数。知道了象元的个数和象元的位置就可恢复出原始图像。
四叉树编码法有许多有趣的优点:①容易而有效地计算多边形的数量特征;②阵列各部分的分辨率是可变的,边界复杂部分四叉树较高,即分级多,分辨率也高,而不需要表示许多细节的部分则分级少,分辨率低,因而既可精确表示图形结构又可减少存储量;③栅格到四叉树及四叉树到简单栅格结构的转换比其它压缩方法容易;④多边形中嵌套异类多边形的表示较方便。
四叉树编码的最大特点是转换的不定性,同一形状和大小的多边形可能得出多种不同的四叉树结构,故不利于形状分析和模式识别。但因它允许多边形中嵌套多边形即所谓“洞”的结构存在,使越来越多的GIS工作者对四叉树结构很感兴趣。上述这些压缩数据的方法应视图形的复杂情况合理选用,同时应在系统中备有相应的程序。另外,用户的分析目的和分析方法也决定着压缩方法的选取。